Science & Math
An Unanswered Question
One of the most beautiful and moving of the bird-songs heard throughout the country which [French merchant Nicolas] Denys governed [in 17th-century Acadia], is that of the Veery, or Wilson’s Thrush. The Maliseet Indians of the Saint John River, as Mr. Tappan Adney has recently told us, say this bird is calling Ta-né-li-ain′, Ni-kó-la Dĕn′-i Dĕn′-i?, that is, ‘Where are you going, Nicolas Denys?’ and Mr. Adney thinks this an actual echo from the days of our author.
— From William Francis Ganong’s 1908 introduction to Denys’ Description and Natural History of the Coasts of North America, 1672
Coverup
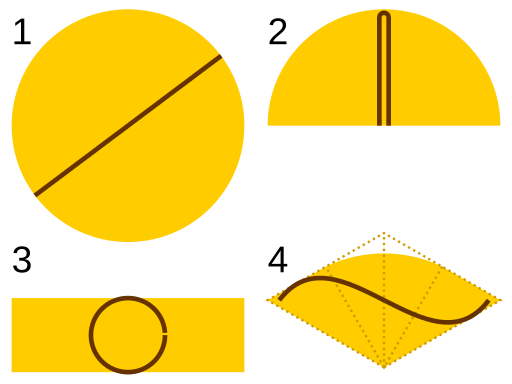
Suppose you have a publicity-seeking inchworm and want to keep him to yourself. What’s the smallest cover you can contrive to keep him hidden? He can writhe into any shape that an inch-long creature can take; you must always be able to turn your shape to keep him covered.
Strangely, we don’t yet know the answer to this question. Mathematician Leo Moser first posed it in 1966, and various proposals have driven the upper bound as low as π/12 ≈ 0.2618, but we still don’t know whether smaller covers are possible. It’s known as Moser’s worm problem.
Early Adopter
At the start of H.G. Wells’ 1895 novella The Time Machine, the Time Traveller explains to his friends that “any real body must have extension in four directions: it must have Length, Breadth, Thickness, and — Duration.” This idea, of conceiving time as a fourth dimension, had been broached in the 18th century, but it had first been treated seriously in a mysterious letter to Nature in 1885:
“I [propose] to consider Time as a fourth dimension of our existence. … Since this fourth dimension cannot be introduced into space, as commonly understood, we require a new kind of space for its existence, which we may call time-space.”
The letter writer identified himself only as “S.” Was this Wells? Apparently not: In his 1934 Experiment in Autobiography Wells wrote, “In the universe in which my brain was living in 1879 there was no nonsense about time being space or anything of that sort. There were three dimensions, up and down, fore and aft and right and left, and I never heard of a fourth dimension until 1884 or there-about. Then I thought it was a witticism.”
So someone had anticipated Wells’ idea by a full decade. As far as I know, his identity has never been discovered.
(Via Paul J. Nahin, Holy Sci-Fi!, 2014.)
Round and Square
This rank impossibility by Kokichi Sugihara won second prize in the Neural Correlate Society’s 2016 illusion of the year contest.
The key is that the top of each cylinder is not a planar curve. Dickinson College mathematician David Richeson has created an interactive applet that you can use to examine the shape, and see his paper below for an explanation of the math and the template of a paper model.
(David Richeson, “Do the Math!: Sugihara’s Impossible Cylinder,” Math Horizons 24:1 [September 2016], 18-19.)
Reciprocity Redux
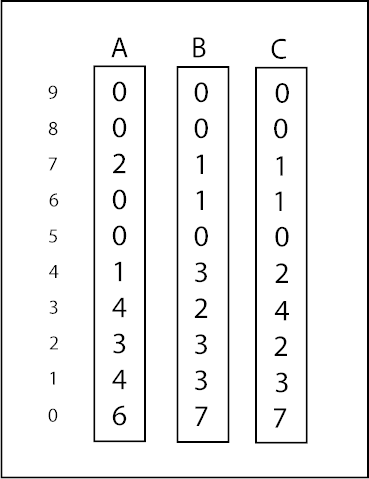
From Lee Sallows:
“The above three strips of ten numbers have an intriguing property. They record how many times each of the decimal digits (shown at left) occur in the other two strips. Hence the 6 in the left-hand strip identifies the number of 0’s in strips B and C, while the 2 in the centre strip counts the number of 3’s present in strips A and C. Moreover, the same property holds for every number in all three strips.”
See Reciprocation.
(Thanks, Lee.)
Org Chart

Say what you will about hell, it’s very well organized. According to the 17th-century grimoire Ars Goetia, the underworld is ruled by 72 demons, each with its own sigil (above) and served by a sort of infernal bureaucracy:
Aim (also Aym or Haborym) is a Great Duke of Hell, very strong, and rules over twenty-six legions of demons. He sets cities, castles and great places on fire, makes men witty in all ways, and gives true answers concerning private matters. He is depicted as a man (handsome to some sources), but with three heads, one of a serpent, the second of a man, and the third of a cat to most authors, although some say of a calf, riding a viper, and carrying in his hand a lit firebrand with which he sets the requested things on fire.
Wikipedia has a page explaining who does what.
Related: Belphegor’s prime, 1000000000000066600000000000001, is a palindromic prime number with 666 at its heart and 13 zeros on either side. It was discovered by Harvey Dubner; Clifford Pickover named it after a prince of hell responsible for helping people make ingenious inventions and discoveries.
It’s A Small World After All
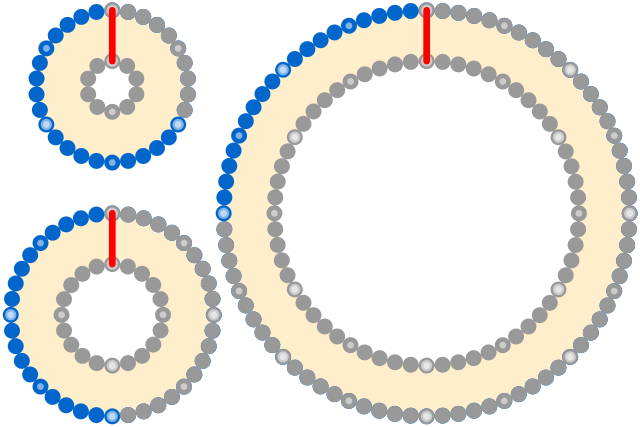
A popular mathematical puzzle asks: Suppose Earth were perfectly spherical and wrapped with a string at the equator. If we wanted to raise the string 1 meter off the ground, all around the world, how much longer would it need to be?
Surprisingly, the answer is only about 6.3 meters. A circle of radius r has a circumference of 2πr. We’re adding a meter to the radius, so the circumference increases by 2π meters.
Even more remarkably, this remains true regardless of the size of the sphere. Above, the increase in the circumference (blue) remains the same for a sphere of any size — it’s determined entirely by the additional radius (red).
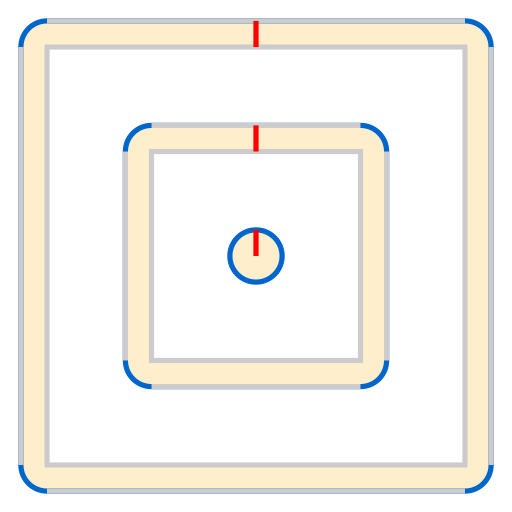
The shape need not even be a sphere! Below, when the string is raised one meter (red) outward from the perimeter of either square, the string’s total length increases only by the combined length of the four blue arcs, which together equal the circumference of a circle of radius 1, or 2π meters.
Monkey Don’t

The infinite monkey theorem holds that a monkey typing at random for an infinite amount of time will almost certainly produce the works of Shakespeare.
This may be true, but mathematicians Stephen Woodcock and Jay Falletta of the University of Technology Sydney find that it would take an extraordinarily long time — longer, in fact, than the life span of the universe.
Assuming a typing speed of one character per second on a 30-key keyboard, they find, a single chimp has only about a 5 percent chance of typing BANANAS in its own lifetime. And even the entire global population of 200,000 chimps will almost certainly never string together the 884,647 words that make up Shakespeare’s works within 10100 years.
“There are many orders of magnitude difference between the expected numbers of keys to be randomly pressed before Shakespeare’s works are reproduced and the number of keystrokes until the universe collapses into thermodynamic equilibrium,” the authors conclude. “As such, we reject the conclusions from the Infinite Monkeys Theorem as potentially misleading within our finite universe.”
Speaking of Shakespeare: Grand Theft Hamlet is a British documentary about the staging of a production of Hamlet inside Grand Theft Auto:
Winner of the Jury Award for best documentary feature at the 2024 SXSW Film Festival, it will be released in the U.K. in December and globally early next year.
(Thanks, John.)
The Unknotting Problem
The least knotted of all knots is a simple closed loop, the “unknot.” Certainly this is easy to spot on its own, but adding even a few twists can make it hard to recognize:
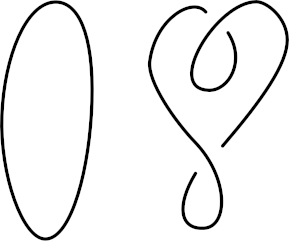
An elaborately draped loop can be quite difficult to distinguish from a knottier knot. Is this an unknot?
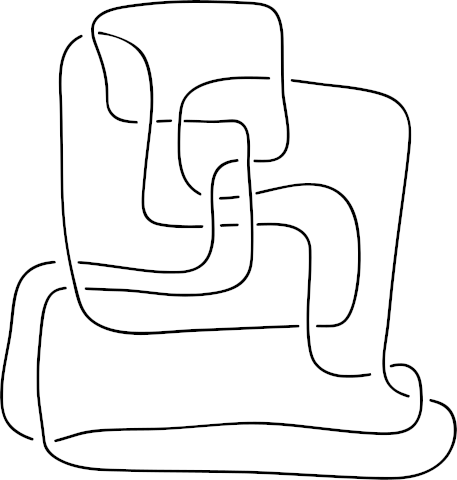
(Yes, it is.)
Surprisingly, while research is ongoing, it remains unknown whether the challenge of recognizing unknots is efficiently solvable — whether an algorithm can accomplish the task in polynomial time. It’s an open question.

