Consider the set (2, 5, 9, 13). Which of these numbers can be tossed out, and for what reason?

We might choose:

• 2 because it’s the only even number.
• 9 because it’s the only non-prime.
• 13 because it doesn’t fit in the sequence A_n – A_n-1 = 1 + (A_n-1 – A_n-2).

“Hence one could toss out either 2, 9 or 13,” observes Marquette University mathematician George R. Sell. “Therefore one should toss out 5 because it is the only number that cannot be tossed out.”

(George R. Sell, “A Paradox,” Pi Mu Epsilon Journal 2:6 [Spring 1957], 278.)

Another amazing contribution by Lee Sallows:

“The picture above shows a 4×4 geomagic square, which is to say a magic square using geometrical shapes that can be fitted together so as to form an identical target shape, in this case a 4×6 rectangle, rather than numbers adding to a constant sum. In addition, the square is also panmagic, meaning that besides the usual 4 rows, 4 columns, and both main diagonals, the shapes occupying each of the so-called ‘broken’ diagonals, afkn, dejo, cfip, bglm, chin, belo, are also able to tile the rectangle. Lastly, the 4 shapes contained in the corner cells of the four embedded 3×3 sub-squares, acik, bdjl, fhnp, egmo, are also ‘magic’, bringing the total number of target-tiling shape sets to 20, a small improvement over the 16 achieved by a panmagic-only square. With that said, it is worth noting that 4×4 geomagic squares have been found achieving target-tiling scores as high as 48.”

Click the image to expand it. Thanks, Lee!

A disease is spreading rapidly across the country. Half the people who have contracted it have died, and half have recovered on their own. A crash program to ward off the epidemic has produced two serums, A and B, but there’s been little time to test them. All three of the patients who were given serum A recovered, and so did 7 of the 8 patients who were given serum B. Unfortunately, you’ve just learned that you have the disease. If you get no treatment, your chances of surviving are 50-50. Both serums have a better record than that, but which one should you take?

“There doesn’t seem to be anything we can do other than appeal to our intuitive feelings on the matter,” writes University of Waterloo mathematician Ross Honsberger. “However, a very ingenious notion, the so-called ‘null hypothesis,’ permits a measure of analysis which, in this case, yields a definite preference.”

The key is to ask how likely it is that 3 out of 3 patients would have recovered if serum A were neither helping nor hindering them. An untreated patient has a 50-50 chance of recovery, so the answer is

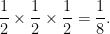
On the other hand, if serum B had no effect, then the chance of 7 recoveries out of 8 is

(Here the factor 8 reflects the fact that there are 8 different possible victims, and again the probability of dying is 1/2.)

So the available evidence suggests that it’s 4 times as likely that serum A has no effect as that serum B has no effect. Your best course is to take serum B.

(Ross Honsberger, “Some Surprises in Probability,” in his Mathematical Plums, 1979.)

The 1968 Putnam Competition included a beautiful one-line proof that π is less than 22/7, its common Diophantine approximation:

The integral must be positive, because the integrand’s denominator is positive and its numerator is the product of two non-negative numbers. But it evaluates to 22/7 – π — and if that expression is positive, then 22/7 must be greater than π.

University of St Andrews mathematician G.M. Phillips wrote, “Who will say that mathematics is devoid of humour?”

On a standard calculator keypad like the one shown here, any four-digit number that is typed in a rectangular shape is evenly divisible by 11. Some examples: 7964, 6523, 1793, 7128. (The numbers must not include 0.)

Parallelograms work too: 1562, 6875, 2783, etc.

Discussion and some proofs here.

09/20/2023 More: Take three digits in order from any row, column, or main diagonal and append the same three digits in reverse order (e.g., 951159). The resulting number will always be evenly divisible by 37 (and, indeed, by 1221). Mathematical Gazette, December 1986 and June 1987. See also A Keypad Oddity.

Once I read a book of 100 numbered pages with one sentence on each page. Page 1: ‘The sentence on page 2 is true.’ Page 2: ‘The sentence on page 3 is true.’ And so on to page 100: ‘The sentence on page 1 is false.’

On the second reading, page 100 changes the entire book. If page 1 is false, then the truth is ‘The sentence on page 2 is false.’ Likewise, page 2 becomes ‘The sentence on page 3 is false.’ And so on to page 100, which now should be read as ‘The sentence on page 1 is true.’

What happens on the third reading?

— David Morice, “Kickshaws,” Word Ways 26:1 (February 1993), 44-55. See Yablo’s Paradox.

Can a chess knight visit every square on a board with 4 rows by a series of successive moves?

No, it can’t, and Hungarian mathematics prodigy Louis Pósa proved this while still in his early teens. Suppose that such a tour is possible. Then, on any board bearing the standard checkerboard pattern, the knight will land alternately on white and black squares. But now imagine that the board’s top and bottom rows have been colored red and the middle two rows are blue. Now a knight on any red square must jump to a blue square, and because the board has an equal number of red and blue squares, any knight on a blue square must jump to a red one (if it visits two blue squares in a row, it won’t be able to make up for this later by visiting two red ones in a row). So the knight’s tour on any 4 × n board must alternate strictly between red and blue squares.

“But this is impossible,” notes Colorado College mathematician John J. Watkins. “The same knight’s tour alternated between white and black squares in the one coloring, and between red and blue squares in the other coloring, which would mean the two color patterns must be the same, which of course they aren’t. Isn’t that a clever proof, especially for a teenager to discover?”

(John J. Watkins, Across the Board, 2004. Pósa’s proof is given more rigorously here, and it’s also presented in Ross Honsberger’s 1973 book Mathematical Gems.)

UPDATE: It’s important to note that it’s a “closed” knight’s tour that’s impossible — that’s one that ends where it began. An open tour, which can end anywhere, is possible — it breaks Pósa’s proof because it need not alternate strictly between red and blue squares. Thanks to reader Marjan Milanović for pointing this out.