“Moreover, the satellites of Jupiter are invisible to the naked eye, and therefore can exercise no influence over the Earth, and therefore would be useless, and therefore do not exist.” — Astronomer Francesco Sizzi, on Galileo’s claim to have seen the moons of Jupiter
Science & Math
Power Tie
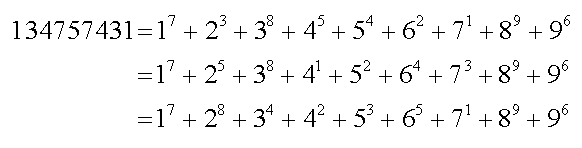
Timeless Reason
In an 1849 letter to his sister, Lewis Carroll asks which is more accurate, a clock that is right once a year or one that has stopped altogether. The stopped clock is more accurate, he says–because it’s correct twice a day.
You might go on to ask, ‘How am I to know when eight o’clock does come? My clock will not tell me.’ Be patient, reader: you know that when eight o’clock comes your clock is right; very good; then your rule is this: keep your eye fixed on your clock, and the very moment it is right it will be eight o’clock.
“‘But–‘ you say. There, that’ll do, reader; the more you argue the farther you get from the point, so it will be as well to stop.”
Truthful Numbers
- FOUR contains four letters.
- TEN is spelled with ten raised dots in Braille.
- TWELVE is worth 12 points in Scrabble.
- FIFTEEN is spelled with 15 dots and dashes in International Morse Code.
TWENTY-NINE contains 29 straight lines — if you don’t count the hyphen.
Fastball
At the 1939 World’s Fair, San Francisco Seals catcher Joe Sprinz tried to catch a baseball dropped from the Goodyear blimp 1,200 feet overhead.
Sprinz knew baseball but he hadn’t studied physics — he lost five teeth and spent three months in the hospital with a fractured jaw.
Cancel That
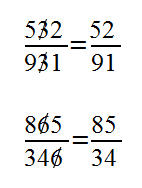
Math Notes
3685 = (36 + 8) × 5
Equivalent Expressions
What do these sentences have in common?

They’re all precisely the same length.
Proof That 3 = 5
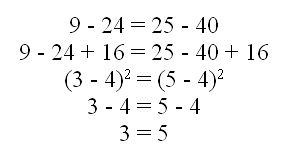
The Doctrinal Paradox
You’re overseeing a murder trial. The defendant will be hanged if his crime is judged to be both willful and premeditated. You poll the jurors:
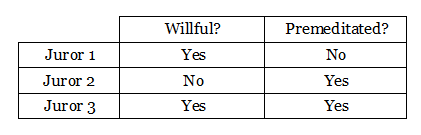
A majority think it was willful, and a majority think it was premeditated, so you order the death penalty. As he’s dragged off to the gallows, the defendant screams that this is unfair and swears that his ghost will return for revenge.
You think nothing more of this until the evening, when a strange thought occurs to you. If you’d simply asked the jurors, “Should this man receive the death penalty?”, most would have voted no — only one of the three jurors believed that the crime was both willful and premeditated. Was your own reasoning unsound?
And who’s that behind you — ?
