In 1885, Cecilia Garrett Smith and a friend were experimenting with automatic writing using a primitive Ouija board on which a planchette was guided by a visiting “spirit.”
“We got all sorts of nonsense out of it, sometimes long doggerel rhymes with several verses,” but the prophecies they asked for were rarely answered. When they asked who the guiding spirit was, the planchette wrote that his name was Jim and that he had been Senior Wrangler at Cambridge. Intrigued, they asked Jim to write the equation describing the heart-shaped planchette they were using, and they received this response:
This they interpreted as 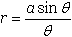 , which J.W. Sharpe later graphed thus:
, which J.W. Sharpe later graphed thus:
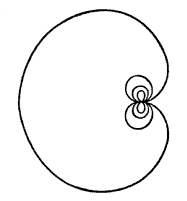
“I am quite sure that I had never seen the curve before, and therefore the production of the equation could not have been an act of unconscious memory on my part,” Smith wrote later. “Also I most certainly did not know enough mathematics to know how to form an equation which would represent such a curve, or to know even of what type the equation must be.”
One wonders what Jim thought of all this. They never got any further math out of him.