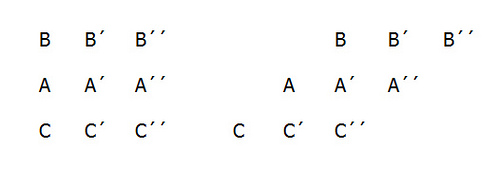
Bertrand Russell explains Zeno’s paradox of the stadium:
Let us suppose three drill-sergeants, A, A′, and A′′, standing in a row, while the two files of soldiers march past them in opposite directions. At the first moment which we consider, the three men B, B′, B′′, in one row, and the three men C, C′, C′′ in the other row, are respectively opposite to A, A′, and A′′. At the very next moment, each row has moved on, and now B and C′′ are opposite A′. When, then, did B pass C′? It must have been somewhere between the two moments which we supposed consecutive. It follows that there must be other moments between any two given moments, and therefore that there must be an infinite number of moments in any given interval of time.
In other words, if time is a series of consecutive instants, and motion means passing through consecutive points, then the Bs are passing the As at the fastest possible speed — one point per instant. How then is it that the Bs are passing the Cs at twice this rate? It seems, Aristotle noted, that “half the time is equal to its double.”
