A puzzle by James Tanton:
King Tricho lives in a palace in which every room is a triangle:
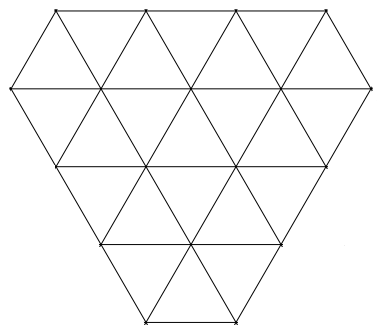
Before retiring for the night he’d like to inspect it. Is there a path that will let him visit each room once and only once? He can start anywhere.
A puzzle by James Tanton:
King Tricho lives in a palace in which every room is a triangle:

Before retiring for the night he’d like to inspect it. Is there a path that will let him visit each room once and only once? He can start anywhere.

A wine merchant has three sons. When he dies, he leaves them seven barrels that are full of wine, seven that are half-full, and seven that are empty. His will requires that each son receive the same number of full, half-full, and empty barrels. Can this be done?
In his 1976 book 100 Numerical Games, French puzzle maven Pierre Berloquin asks whether it’s possible to construct a magic square using the first nine prime numbers (here counting 1 as prime):
1 2 3 5 7 11 13 17 19
Is it?

Here are five new lateral thinking puzzles to test your wits and stump your friends — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
ullage
n. the amount a container lacks of being full
Given a 5-gallon jug, a 3-gallon jug, and a limitless supply of water, how can you measure out exactly 4 gallons?
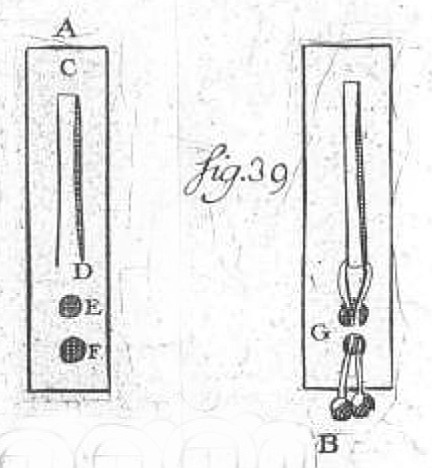
A classic puzzle from Jacques Ozanam’s Recreations Mathematiques et Physiques, 1723. Two slits (CD) and two holes (EF) are cut in a slip of paper, and a cherry stem is suspended as shown. The cherries are too large to fit through the holes. How can you free the stem and its cherries intact from the slip?