Science & Math
Bang’s Theorem on Tetrahedra
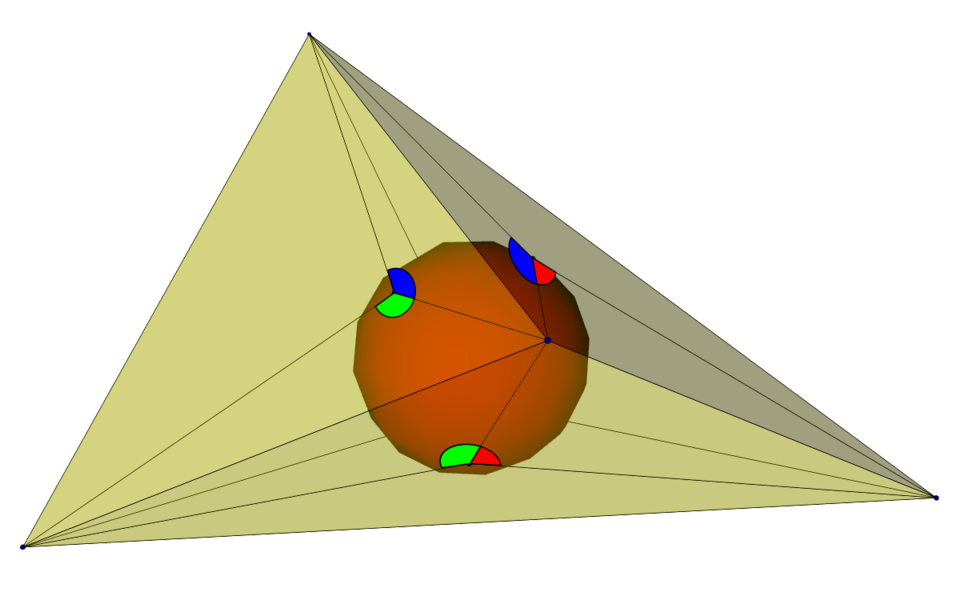
If a sphere is inscribed in a tetrahedron, and segments are drawn on each face connecting its vertices to the point of tangency, then the same three angles will appear on each face.
And the 12 triangles produced will form congruent pairs across each edge of the tetrahedron.
The Ross-Littlewood Paradox
Into an empty vase drop balls numbered 1 to 10. Remove ball 1. Add balls numbered 11 to 20. Remove ball 2. Continue in this way, spending half an hour on the first transaction, 15 minutes on the next, and so on. After one hour all the transactions will be finished.
Obviously, in the end the vase will contain infinitely many balls, since with each step more balls have been added than removed.
But, equally obviously, after an hour the vase will be empty — since the time of each ball’s removal is known.
Getting Started
He, then, who says that something true exists either only asserts that something true exists or proves it. And if he merely asserts it, he will be told the opposite of his mere assertion, namely, that nothing is true. But if he proves that something is true, he proves it either by a true proof or by one that is not true. But he will not say that it is by one not true, for such a proof is not to be trusted. And if it is by a true proof, whence comes it that the proof which proves that something is true is itself true? If it is true of itself, it will be possible also to state as true of itself that truth does not exist; while if it is derived from proof, the question will again be asked ‘How is it that this proof is true?’ and so on ad infinitum. Since, then, in order to learn that there is something true, an infinite series must first be grasped, and it is not possible for an infinite series to be grasped, it is not possible to know for a surety that something true exists.
— Sextus Empiricus, Against the Logicians
String Theory
In the classic Indian rope trick, a rope rises into the sky, its end lost to view. A boy disappears up the rope, and when he fails to return the angry magician climbs up after him. Body parts fall to the ground, the magician descends and places the parts in a basket, and the boy reappears uninjured.
This is all thought to be a legend, but in 1979 mathematician J.L.G. Pinhey of The Perse Boys’ School worked out that levitating a rope is possible, at least in principle. If the top of the fakir’s rope is 1.5 × 108 meters above Earth’s surface, it will simply stand erect, its position sustained by the motion of the planet.
“Since the rope between its ends is in tension the configuration is stable, and the faqir and his boy-victim can climb it in safety. However, in order to drop the bits to earth, the pair must not climb even a quarter of the way to the top.”
(J.L.G. Pinhey, “63.12 The Indian Rope Trick,” Mathematical Gazette 63:424 [June 1979], 110-111.)
Misc
- In the King James Bible, Ezra 7:21 lacks only the letter J, and 1 Chronicles 12:40 lacks only Q.
- In 2016 Pharmacy Times judged talimogene laherparepvec the hardest drug name to pronounce.
- 34 × 72 × 875 = 3472875 (B.J. van der Zwaag)
- The Estonian word kuulilennuteetunneliluuk (“bullet tunnel hatch”) is a palindrome.
- “No one ever forgets where he buried the hatchet.” — Kin Hubbard
Finger Math
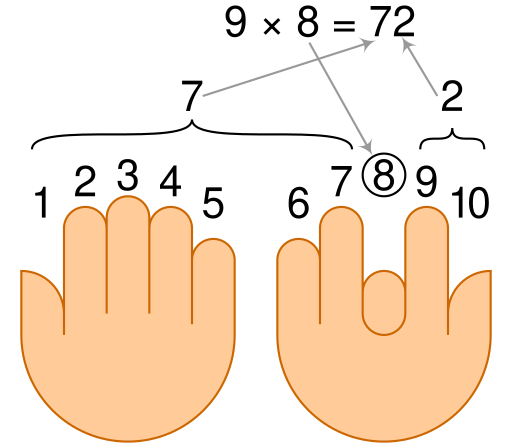
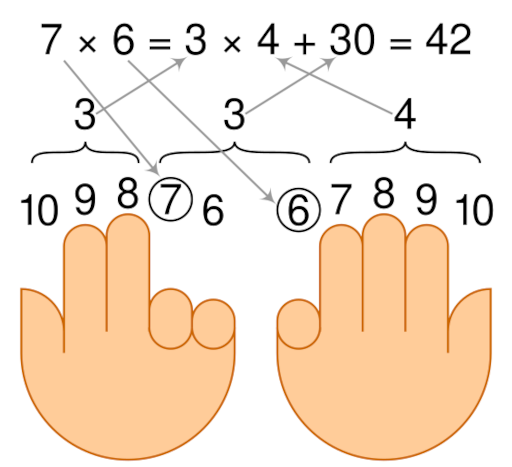
From Wikimedia user Cmglee, two digital arithmetic techniques:
Above: To multiply a positive single-digit integer by 9, hold up your hands palm up, imagine the fingers numbered consecutively 1 to 10, and fold down the finger corresponding to the number to be multiplied (here, 8). The product is the two-digit number represented by the remaining two groups of fingers — here there are seven fingers to the left of the folded finger and 2 to the right, so 9 × 8 = 72.
Below: To multiply two integers between 6 and 10, imagine each hand’s fingers numbered from 6 (pinky) to 10 (thumb), as shown. Fold down the two fingers corresponding to the factors, as well as all fingers between these two (in this example we’ll calculate 6 × 7, so fold down finger 7 on the left hand, finger 6 on the right, and the finger that lies between them, the left pinky). Count the remaining upraised fingers on the left hand (3), multiply that by the remaining upraised fingers on the right hand (4), and add 10 times the number of folded fingers (30). 3 × 4 + 30 = 42.
Monsky’s Theorem
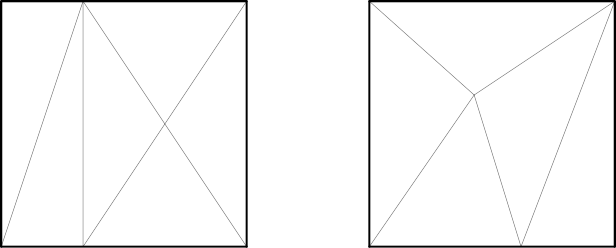
A square can be divided into an even number of triangles of equal area — but not into an odd number.
Uh-Oh
Every unjust act is inexpedient;
No unjust act is expedient;
No expedient act is unjust;
Therefore every expedient act is just.
— Ralph L. Woods, How to Torture Your Mind, 1969
Horseplay
I just found this in a 1950 issue of Pi Mu Epsilon Journal:
Question: How many legs has a horse?
Answer: Twelve; two in front, two behind, two on each side, and one in each corner.
Later in the same volume, Marlow Sholander shows that in fact every horse has an infinite number of legs.
That’s to say nothing of color. And see Chasing Leo.