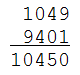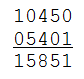Stigler’s Law of Eponymy states that “no scientific discovery is named after its original discoverer.” Examples:
- Arabic numerals were invented in India.
- Darwin lists 18 predecessors who had advanced the idea of evolution by natural selection.
- Freeman Dyson credited the idea of the Dyson sphere to Olaf Stapledon.
- Salmonella was discovered by Theobald Smith but named after Daniel Elmer Salmon.
- Copernicus propounded Gresham’s Law.
- Pell’s equation was first solved by William Brouncker.
- Euler’s number was discovered by Jacob Bernoulli.
- The Gaussian distribution was introduced by Abraham de Moivre.
- The Mandelbrot set was discovered by Pierre Fatou and Gaston Julia.
University of Chicago statistics professor Stephen Stigler advanced the idea in 1980.
Delightfully, he attributes it to Robert Merton.