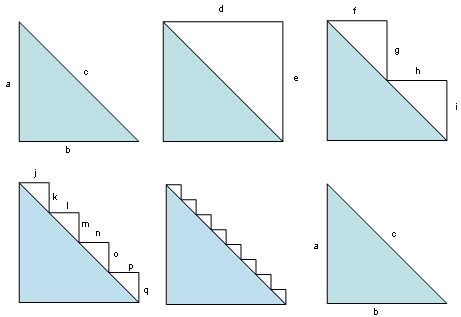
Draw a right triangle whose legs a and b each measure 1. Draw d and e to complete a unit square. Clearly d + e = 2.
Now if we cut a “step” into the square as shown, then f + h = 1 and g + i = 1, so the total length of the “staircase” is still 2. Cut still finer steps and j + k + l + m + n + o + p + q is likewise 2.
And so on: The more finely we cut the steps, the more closely their shape approximates that of the original triangle’s diagonal. Yet the total length of the stairstep shape remains 2, the sum of its horizontal and vertical elements. At the limit, then, it would seem that c must measure 2 … but we know that the length of a unit square’s diagonal is the square root of 2. Where is the error?
(Thanks, Alex.)