Puzzles
Black and White
Trivium
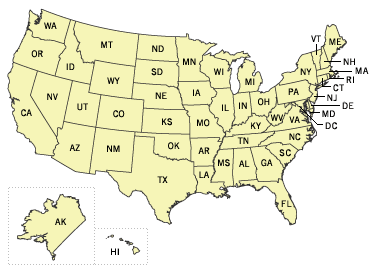
The names of two U.S. state capitals end with the same eight letters. What are they?
Black and White
“Anglo-Foreign Words”
Walter Penney of Greenbelt, Md., offered this poser in the August 1969 issue of Word Ways: The Journal of Recreational Linguistics. Below are five groups of English words. Each group appears also in a foreign language. What are the languages?
- aloud, angel, hark, inner, lover, room, taken, wig
- alas, atlas, into, manner, pore, tie, vain, valve
- ail, ballot, enter, four, lent, lit, mire, taller
- banjo, chosen, hippo, pure, same, share, tempo, tendon
- ago, cur, dare, fur, limes, mane, probe, undo
Projective Chess
In projective geometry, every family of parallel straight lines intersects at an infinitely distant point. Chess problem composers in the former Yugoslavia have adapted this idea for the chessboard, adding four special squares “at infinity.”
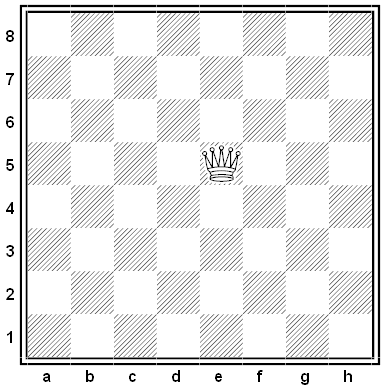
Now a queen on a bare board, for example, can zoom off to the west (or east) and reach a square “at infinity” from which she attacks every rank on the board simultaneously from both directions. She might also zoom to the north (or south) to reach a different square at infinity; from this one she attacks every file simultaneously, again from both directions. Finally she can zoom to the northwest or southeast and attack all the diagonals parallel to a8-h1, or zoom to the northeast or southwest and attack all the diagonals parallel to a1-h8. These four “infinity squares,” plus the regular board, make up the field of play.
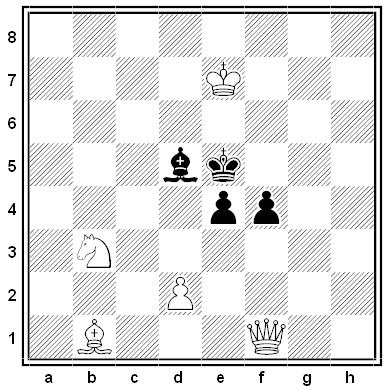
N. Petrovic created the problem below, published in Matematika Na Shahmatnoi Doske. White is to play and mate in at least two moves. Can you find the solution?

Reunion

A Russian problem from the 1999 Mathematical Olympiad:
A father wants to take his two sons to visit their grandmother, who lives 33 kilometers away. His motorcycle will cover 25 kilometers per hour if he rides alone, but the speed drops to 20 kph if he carries one passenger, and he cannot carry two. Each brother walks at 5 kph. Can the three of them reach grandmother’s house in 3 hours?
Black and White
Calendar Trouble
From Sam Loyd:
Two children, who were all tangled up in their reckoning of the days of the week, paused on their way to school to straighten matters out.
“When the day after tomorrow is yesterday,” said Priscilla, “then ‘today’ will be as far from Sunday as that day was which was ‘today’ when the day before yesterday was tomorrow!”
On which day of the week did this puzzling prattle occur?
Crime Story
Six boys are accused of stealing apples. Exactly two are guilty. Which two? When the boys are questioned, Harry names Charlie and George, James names Donald and Tom, Donald names Tom and Charlie, George names Harry and Charlie, and Charlie names Donald and James. Tom can’t be found. Four of the boys who were questioned named one guilty boy correctly and one incorrectly, and the fifth lied outright. Who stole the apples?