In projective geometry, every family of parallel straight lines intersects at an infinitely distant point. Chess problem composers in the former Yugoslavia have adapted this idea for the chessboard, adding four special squares “at infinity.”

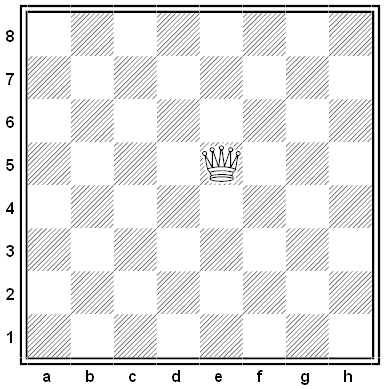
Now a queen on a bare board, for example, can zoom off to the west (or east) and reach a square “at infinity” from which she attacks every rank on the board simultaneously from both directions. She might also zoom to the north (or south) to reach a different square at infinity; from this one she attacks every file simultaneously, again from both directions. Finally she can zoom to the northwest or southeast and attack all the diagonals parallel to a8-h1, or zoom to the northeast or southwest and attack all the diagonals parallel to a1-h8. These four “infinity squares,” plus the regular board, make up the field of play.

N. Petrovic created the problem below, published in Matematika Na Shahmatnoi Doske. White is to play and mate in at least two moves. Can you find the solution?