In Henry Dudeney’s Canterbury Puzzles, Sir Hugh De Fortibus takes his chief builder to the walls of his donjon keep and points to a window there.
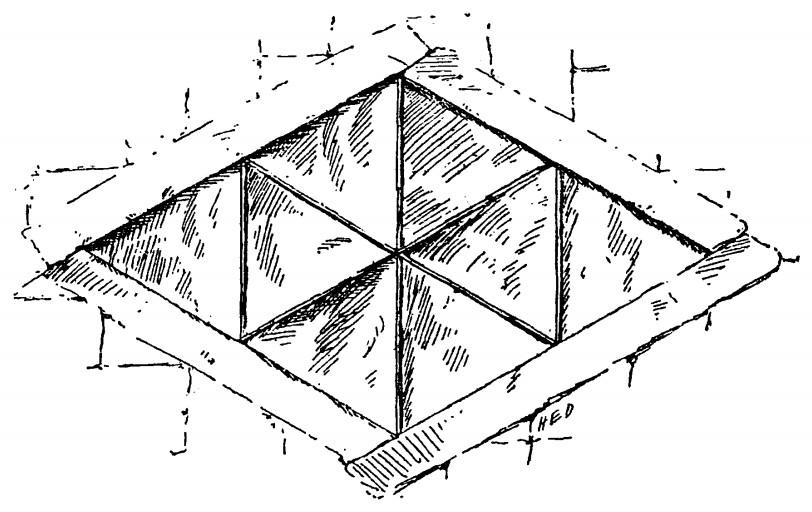
“Methinks,” he says, “yon window is square, and measures, on the inside, one foot every way, and is divided by the narrow bars into four lights, measuring half a foot on every side.”
“Of a truth that is so, Sir Hugh,” says the builder.
“Then I desire that another window be made higher up whose four sides shall also be each one foot, but it shall be divided by bars into eight lights, whose sides shall be all equal.”
Bewildered, the builder says, “Truly, Sir Hugh, I know not how it may be done.”
“By my halidame!” exclaims De Fortibus in pretended rage. “Let it be done forthwith. I trow thou art but a sorry craftsman, if thou canst not, forsooth, set such a window in a keep wall.”
How can it be done?