Suppose some 2n points in the plane are chosen so that no three are collinear, and then half are colored red and half blue. Will it always be possible to connect each red point with a blue one, in pairs, so that none of the connecting lines intersect?
|
SelectClick for Answer |
Yes. Since n is finite, there are a limited number of ways to make the pairings. And for each way of making them, the lengths of the n segments add up to some total amount.
Now, if an arrangement contains an intersection, this total length can be reduced by an appeal to the triangle inequality, which says that the sum of the lengths of any two sides of a triangle must be greater than the third side.
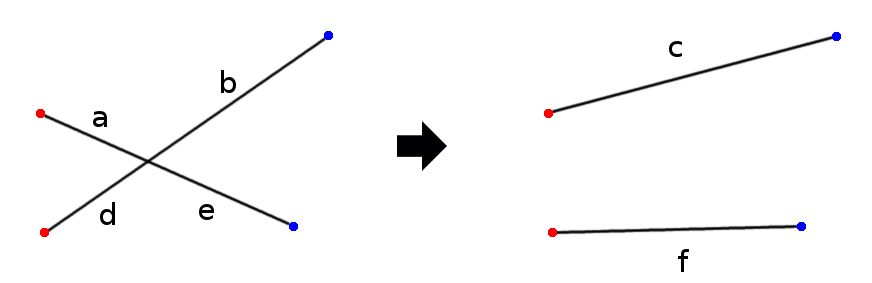
In the example above, if we reassign the connections as shown, the total length of the connecting segments is reduced, because c < a + b and f < d + e.
Hence the arrangement with the minimum total length must necessarily be free of intersections.
(A Putnam paper problem from 1979, via Ross Honsberger’s Mathematical Gems, 1985.)
09/04/2016 Reader Jacob Bandes-Storch shows one way to establish the pairings.
|

