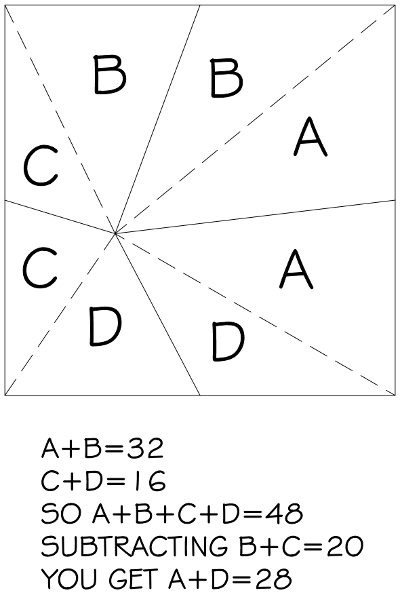
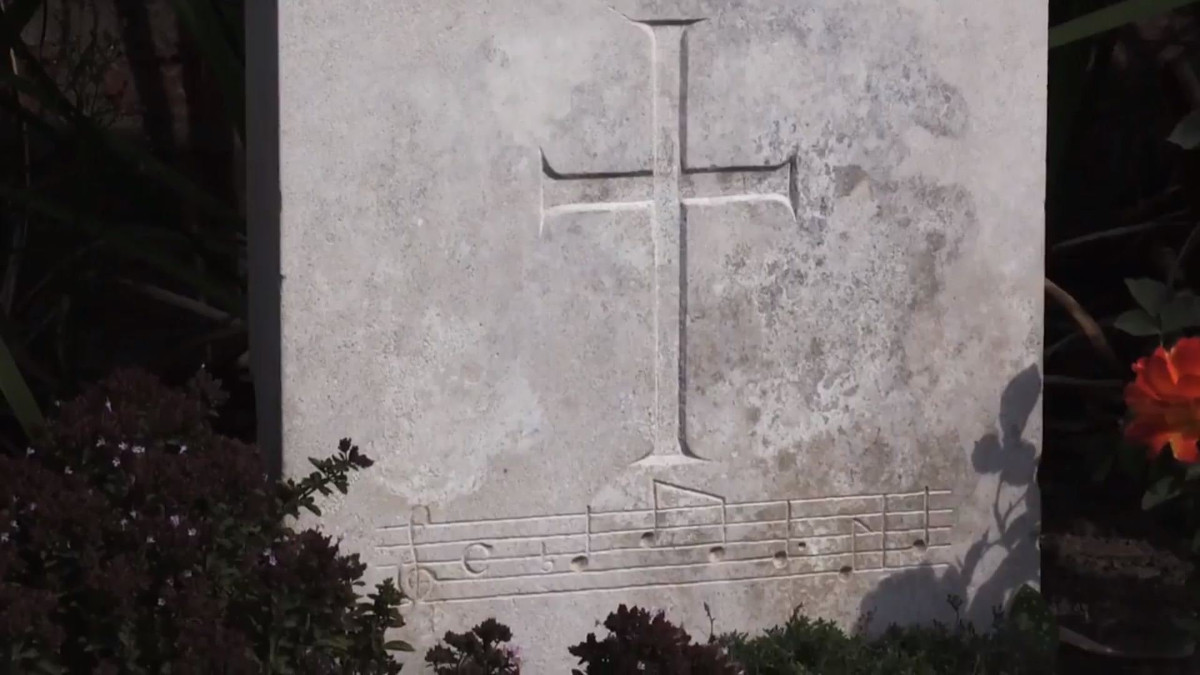A puzzle by University College London mathematician Matthew Scroggs: A princess lives in a row of 17 rooms. Each day she moves to a new room adjacent to the last one (e.g., if she sleeps in Room 5 on one night, then she’ll sleep in Room 4 or Room 6 the following night). You can open one door each night. If you find her you’ll become her prince. Can you find her in a finite number of moves?
Puzzles
Sanity Check

From Raymond Smullyan: Every inhabitant of this island either a knight or a knave. Knights always tell the truth, and knaves always lie. Further, every inhabitant is either mad or sane. Sane inhabitants always answer questions correctly, and mad ones always answer incorrectly. You meet an inhabitant of the island and want to know whether he’s sane or mad. How can you determine this with a single yes-or-no question?
For Pi Day
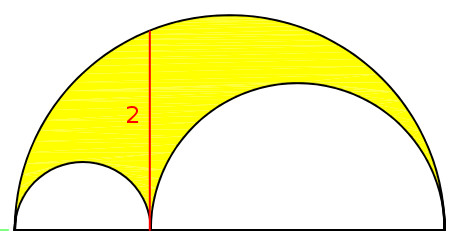
From the prolifically interesting Catriona Shearer: The red line is perpendicular to the bases of the three semicircles. What’s the total area shaded in yellow?
E Pluribus Unum
The THOG Problem
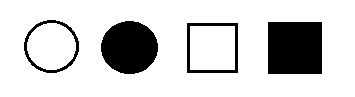
I have picked one color (black or white) and one shape (square or circle). A symbol that possesses exactly one of the properties I have picked is called a THOG. The black circle is a THOG. For each of the other symbols, is it (a) definitely a THOG, (b) undecidable, or (c) definitely not a THOG?
Cognitive psychologist Peter Wason invented this puzzle in 1979 to demonstrate some weaknesses in human thinking. In pilot studies, 0 of 10 student barristers were able to solve it correctly, with one arguing for more than an hour against the correctness of Wason’s solution. Seven of 14 medical students solved it, taking an average of 6.3 minutes. (“This is quite an impressive result.”) One young doctor solved it in his head in about a minute and said, “I would not let any doctor near me who couldn’t solve that problem.” What’s the answer?
Black and White
A Pretty Puzzle
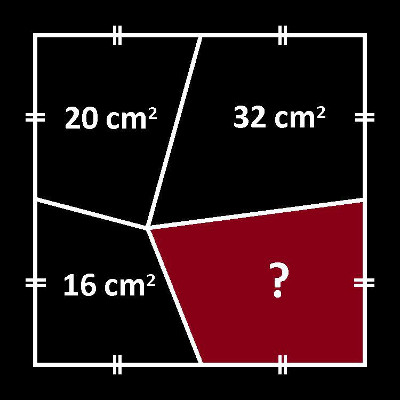
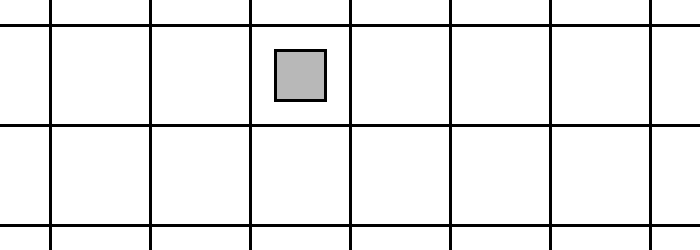
I don’t know who came up with this; I found it on r/mathpuzzles. What’s the area of the red region?
Loose Change
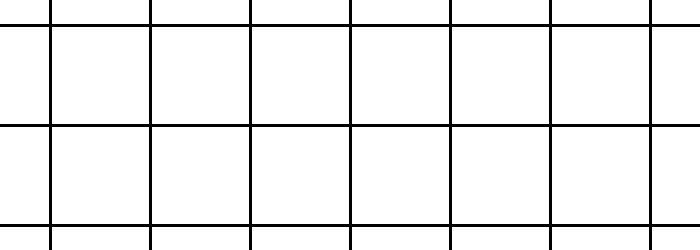
You’re holding a penny, and you’re standing on an infinite plane. The plane bears a grid of squares, each of which is twice the width of the penny. If you roll the penny out onto the grid, what is the probability that it will come to rest entirely within a square? (Assume the lines are of negligible thickness.)
A Memorial Puzzle
When violinist Hugh Gordon Langton was killed in World War I, the Commonwealth War Graves Commission inscribed a phrase of music (below, click to enlarge) on his headstone in Belgium’s Poelcapelle British Cemetery.
What the notes represent has been a mystery for more than a century. “They are not part of a tune that anyone has been able to discern and several have tried,” writes Sarah Wearne in Epitaphs of the Great War: Passchendaele. “In particular they are not from the song ‘After the Ball’ as some have suggested.”
Langton is the only casualty who was commemorated with a piece of music — the CWGC maintains more than a million graves and memorials worldwide, and only this one bears musical notes as an epitaph. If you can identify the tune, please contact the Commission.
A Problem From 1725
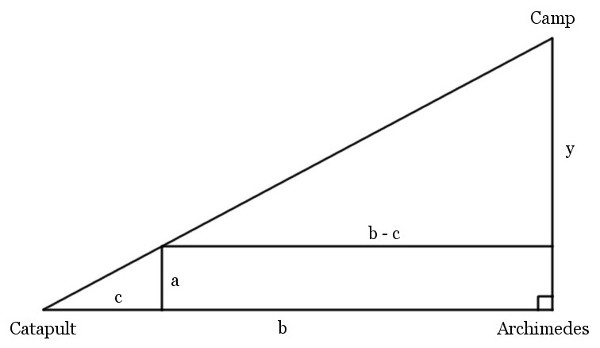
Suppose that when Marcellus besieged Syracuse, Archimedes was standing at a corner of the city wall. A ditch runs parallel to the wall, separated from it by a distance a. To Archimedes’ left at distance b along the wall stands a catapult, which is distance c from a line perpendicular to the ditch. If Archimedes’ line of sight to the camp runs perpendicular to the wall and the ditch, show that he stood a distance ab/c from the camp.