From Pi Mu Epsilon Journal, November 1950:
(1/2)3 < (1/2)2.
Taking the logarithm to the base 1/2 of each member of the above inequality, we write
3 log1/2(1/2) < 2 log1/2(1/2).
But logbb = 1. Therefore
3 < 2.
From Pi Mu Epsilon Journal, November 1950:
(1/2)3 < (1/2)2.
Taking the logarithm to the base 1/2 of each member of the above inequality, we write
3 log1/2(1/2) < 2 log1/2(1/2).
But logbb = 1. Therefore
3 < 2.

Several claimants have been put forth as the originators of the modern tropical cyclone ‘naming’ system. Australian weather meteorologist, Clement L. Wragge, is one of the best-established holders of the title. … Most ingeniously, he gained a measure of personal revenge by christening some of the nastiest storms with politicians’ names such as Drake, Barton, and Deakin. Modern hurricane researcher Chris Landsea noted that, by using such a personal naming system, Wragge could publicly describe a politician (say one who was less than generous with weather-bureau appropriations) as ‘causing great distress’ or ‘wandering aimlessly about the Pacific.’
— Randy Cerveny, Freaks of the Storm, 2006

According to Frank M. Chapman’s Color Key to North American Birds (1912), the hooded warbler sings You must come to the woods, or you won’t see me.
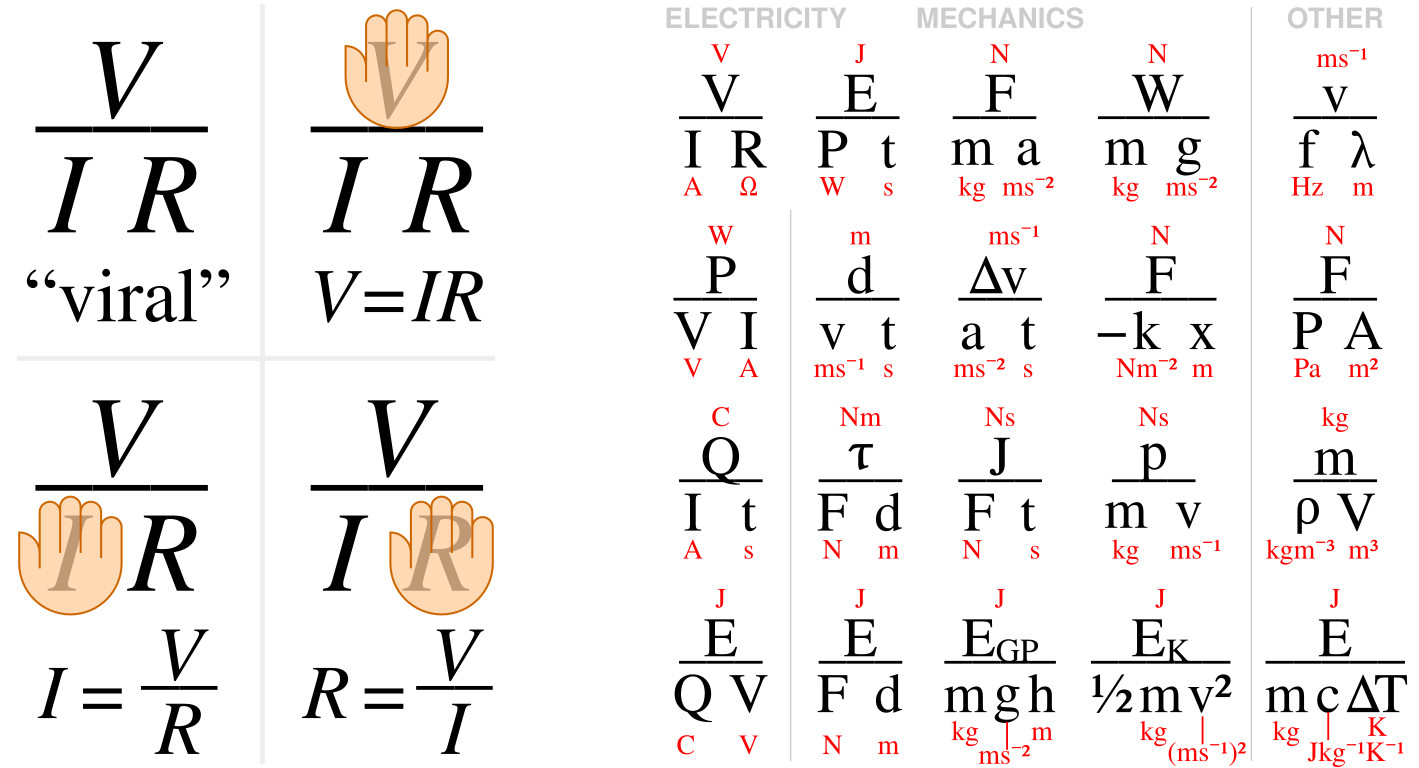
Ohm’s law states that V = IR, where V is the voltage measured across a conductor, I is the current through the conductor, and R is the conductor’s resistance. In the image mnemonic at left (easily remembered by the word “viral”), covering any of the unknowns gives the formula in terms of the remaining parameters: V = IR, I = V/R, R = V/I.
Wikimedia user CMG Lee has devised other mnemonics in the same style for high-school physics students (right). For example, F = ma, m = F/a, a = F/m. In the corresponding SVG file you can hover over a symbol to see its meaning and formula.

An illusion by University of Texas engineer David Novick: All the spheres have the same light-brown base color (RGB 255,188,144). The intervening foreground stripes seem to impart different hues. See this Twitter thread for the same image with the foreground stripes removed.
Have the love and fear of God ever before thine eyes; God confirm your faith in Christ and that you may live accordingly, Je vous recommende a Dieu. If you meet with any pretty insects of any kind keep them in a box.
— Sir Thomas Browne, letter to his son, 1661
If you’re driving on the highway and pass a car traveling in the opposite direction, the frequency of its engine noise seems to drop. In 1980, Liverpool Polytechnic mathematician J.M.H. Peters realized that this pitch drop might be used to estimate the speed of the passing vehicle. Pleasingly, he discovered that each semitone in the interval corresponds to 21 miles per hour (to within 2 percent). If the other car’s engine seems to descend a whole tone in pitch as it passes you, then it’s traveling at approximately 43 mph; if it drops a minor third then it’s traveling at 64 mph; and so on.
“The reader should practise by humming a given note pianissimo increasing gradually to fortissimo at which point the hum is lowered by a chosen interval, … diminishing again to pianissimo, this being meant to imitate the effect of being suddenly passed on a quiet country lane by a fast moving high powered motor vehicle.”
(J.M.H. Peters, “64.8 Estimating the Speed of a Passing Vehicle,” Mathematical Gazette 64:428 [June 1980], 122-124.)
03/03/2025 UPDATE: My mistake — the observer is stationary, not moving. Thanks to readers Seth Cohen and Jon Jerome for pointing this out. The cited paper is behind a paywall, but the Physics Stack Exchange had a discussion on the same topic in 2017.

From Good-Bye to All That, poet Robert Graves’ 1929 account of his experiences in World War I:
Beaumont had been telling how he had won about five pounds’ worth of francs in the sweepstake after the Rue du Bois show: a sweepstake of the sort that leaves no bitterness behind it. Before a show, the platoon pools all its available cash and the survivors divide it up afterwards. Those who are killed can’t complain, the wounded would have given far more than that to escape as they have, and the unwounded regard the money as a consolation prize for still being here.
In 2003, the Journal of Political Economy reprinted this paragraph with the title “Optimal Risk Sharing in the Trenches.”

Every positive integer can be represented uniquely as the sum of one or more distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers.
Above, 51 = 34 + 13 + 3 + 1.
Discovered in 1952 by Dutch mathematician Gerrit Lekkerkerker (and remarked 20 years later by Edouard Zeckendorf).