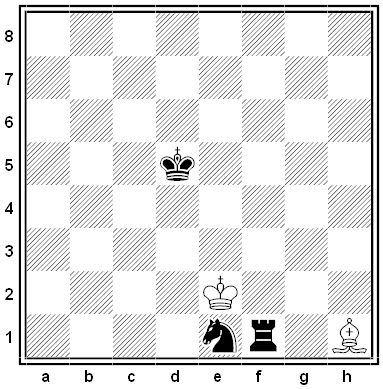
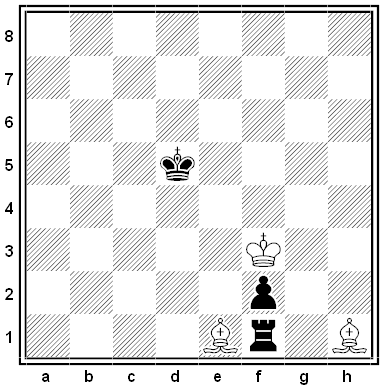
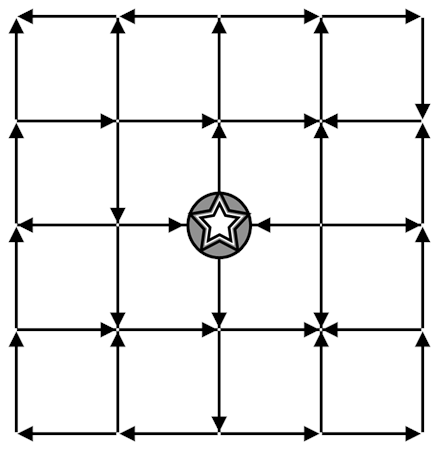
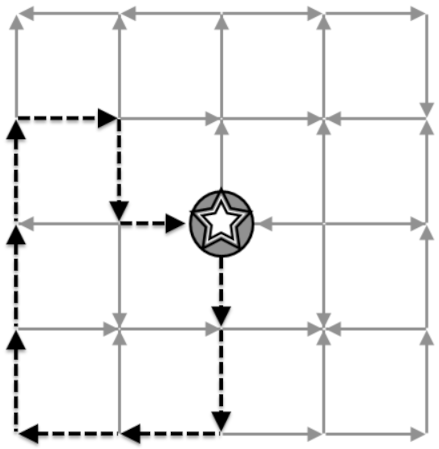
Inspired by the college’s name, each punt evokes the number three:
In the game NOUGHTS & CROSSES, players compete to place three marks in a row.
A CODON is a sequence of three nucleotides in a DNA or RNA molecule.
In Greek mythology, beauty was deified in the three GRACEs Euphrosyne, Aglaia, and Thalia.
A HAIKU has three lines.
Three WISE MONKEYs illustrate the maxim “See no evil, hear no evil, speak no evil.”
NENYA is one of the three Rings of Power in J.R.R. Tolkien’s fantasy legendarium.
FLUFFY is a three-headed dog in J.K. Rowling’s Harry Potter universe.
Traditionally after two failures one hopes for a third LUCKY TIME.
CHARLES III is king of the United Kingdom.
Not shown:
LITHIUM has atomic number 3.
A BARYON is a subatomic particle made up of three quarks.
02/11/2025 UPDATE: Wow, yet more!

The additional names include LITTLE KITTEN, CHEER, BRONZE, WISE MAN, PEACE SWEET, GRUFF, MAD GEORGE, DIABOLUS IN MUSICA, HARRY LIME, and POINT TURN.
(Thanks, Dmitry.)