Puzzles
An Upper Stove
A problem by Soviet physicist Viktor Lange:
“By lifting up a bucket of coal to a third floor stove we increase the potential energy of the coal by about 800 J (the force of gravity on the coal is about 80 N and it is raised by about 10 m). Where will this additional potential energy go to when this coal is burnt in the stove?”
An NSA Puzzle
A problem by National Security Agency mathematician Wendell W., from the agency’s March 2018 Puzzle Periodical:
Consider the following equations:
a2 × b × c2 × g = 5,100
a × b2 × e × f2 = 33,462
a × c2 × d3 = 17,150
a3 × b3 × c × d × e2 = 914,760
Find positive integers a, b, c, d, e, f, and g, all greater than 1, that satisfy all the equations.
“The Difficult Case of Wine”
A gentleman had a bottle containing 12 pints of wine, 6 of which he was desirous of giving to a friend; but he had nothing to measure it, except two other bottles, one of 7 pints, and the other of 5. How did he contrive to put 6 pints into the 7-pint bottle?
Five-Sided Story
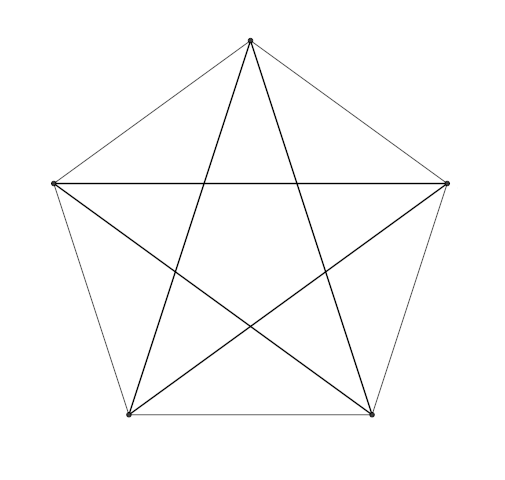
In a regular pentagon, all diagonals are drawn, as shown. Label each vertex of the pentagon and each intersection of the diagonals with the number 1. Now: In one step you can change the signs of all the numbers on a side or on a diagonal. Is it possible, by a sequence of such steps, to convert all the labels in the diagram to -1?
A Crowded Verse
The names of 13 Jane Austen characters are hidden in the following lines as anagrams of complete consecutive words. For example, “was ill” yields WALLIS. (The names to be found are women’s first names and men’s surnames, as in Austen.) In most cases the anagrams are hidden in two words, but twice they’re in three, once in four, and once in a single word. What are they?
The other day when I was ill
And not a soul I knew came nigh,
Jane Austen was my daily fare —
I rather liked to be laid by.
Each line or page enthralls me quite,
I there can let no man deride;
I may be ill as a wight can be,
But, Jane with me, am satisfied.
In bed my ease is nil, yet I’ll
Be lying therein at any rate
Content. With Jane to chortle at
How can I rail at Fate?
Road Trip
A problem from the qualification round of the 2004/2005 Swedish Mathematical Contest, via the April 2009 issue of Crux Mathematicorum:
The cities A, B, C, D, and E are connected by straight roads (more than two cities may lie on the same road). The distance from A to B, and from C to D, is 3 km. The distance from B to D is 1 km, from A to C it is 5 km, from D to E it is 4 km, and finally, from A to E it is 8 km. Determine the distance from C to E.
Black and White

In Two-Move Chess Problems (1986), Robert Moore calls this a “very lightweight jewel.” White to mate in two moves.