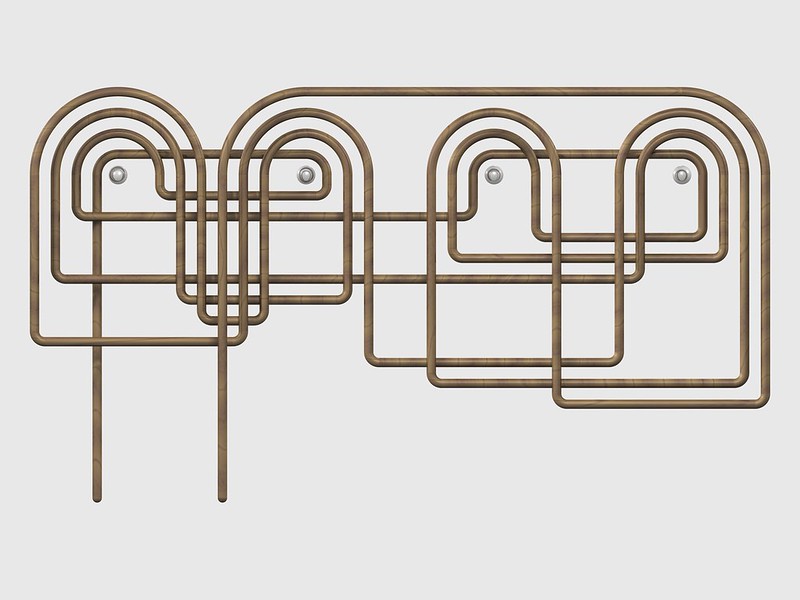
A mathematical oddity: Removing any of these four nails will cause the entire rope to fall.
By Flickr user fdecomite. More at the link below.
(Erik D. Demaine, et al., “Picture-Hanging Puzzles,” Theory of Computing Systems 54:4 [May 2014], 531-550.)

A mathematical oddity: Removing any of these four nails will cause the entire rope to fall.
By Flickr user fdecomite. More at the link below.
(Erik D. Demaine, et al., “Picture-Hanging Puzzles,” Theory of Computing Systems 54:4 [May 2014], 531-550.)
chevelure
n. a head of hair
abditive
adj. hidden
protreptic
n. a writing intended to exhort or instruct
revolute
v. to imbue with revolutionary spirit
For Histiaeus, when he was anxious to give Aristagoras orders to revolt, could find but one safe way, as the roads were guarded, of making his wishes known; which was by taking the trustiest of his slaves, shaving all the hair from off his head, and then pricking letters upon the skin, and waiting till the hair grew again. Thus accordingly he did; and as soon as ever the hair was grown, he despatched the man to Miletus, giving him no other message than this — ‘When thou art come to Miletus, bid Aristagoras shave thy head, and look thereon.’ Now the marks on the head, as I have already mentioned, were a command to revolt.
— Herodotus, Terpsichore

In 1962, determined to start life anew, Yorkshire newspaper editor Brendon Grimshaw purchased little Moyenne Island in the Seychelles for £8,000. He remained there for the next 40 years. In that time Grimshaw and an assistant planted 16,000 trees by hand, built three miles of nature paths, attracted 2,000 new birds, and became caretakers of 120 giant tortoises. The island now hosts two thirds of all plants endemic to the Seychelles.
Grimshaw once turned down an offer of $50 million for the island, saying that he didn’t want to see it become a holiday destination for millionaires. Instead, in 2008 it was named a national park. Grimshaw died in 2012, but today a warden is posted on the island to collect entrance fees from tourists.
From reader Éric Angelini:
Call this S1:
FIRST, SECOND, THIRD, FOURTH, FIFTH, SIXTH, SEVENTH, EIGHTH, NINTH, TENTH, ELEVENTH, …
Consider it both a string of letters and a list of instructions: We are to underline the indicated letters, in order. That’s pretty straightforward — we’ll underline the first letter, then the second, then the third, and so on, ultimately reproducing S1.
Suppose we start the list with SIXTH, rather than FIRST. Now our first instruction is to underline the sixth letter, which is the S in SECOND. After that we underline the second letter in the string, as before, and the third, and so on. Only the very first letter, the F in FIRST, has been overlooked, and we can remedy that by putting FIRST in the sixth position in the list. With that swap all is well:
S6 = SIXTH, SECOND, THIRD, FOURTH, FIFTH, FIRST, SEVENTH, EIGHTH, NINTH, TENTH, ELEVENTH, …
Similarly, if the list starts with EIGHTH we can get everything underlined with just a single swap:
S8 = EIGHTH, SECOND, THIRD, FOURTH, FIFTH, SIXTH, SEVENTH, FIRST, NINTH, TENTH, ELEVENTH, …
Éric asks, “What about starting S9 with NINTH? How many swaps do we need to reproduce S9? This is more tricky!”
See the answer by Hans Havermann at the bottom of this page.
(Thanks, Éric.)

In 2005, philosopher Nicholas Shackel identified a form of argument in which an arguer claims to defend a controversial position while retreating, under pressure, to a more supportable one. He likened it to a medieval castle defense known as the motte and bailey, in which a stone tower, the motte, is surrounded by an area of open land, the bailey. If maurauders invade the bailey, the defender retreats to the motte, and when the attackers have given up he can reoccupy the bailey.
“For my purposes the desirable but only lightly defensible territory of the Motte and Bailey castle, that is to say, the Bailey, represents a philosophical doctrine or position with similar properties: desirable to its proponent but only lightly defensible,” Shackel wrote. “The Motte is the defensible but undesired position to which one retreats when hard pressed.”
By withdrawing as needed to a better-supported claim, a skilled arguer can pretend greater security than he’s established, and even accuse his critics of misrepresenting his position. Other writers have suggested that this is a common tactic in pseudoscience.
(Nicholas Shackel, “The Vacuity of Postmodernist Methodology,” Metaphilosophy 36:3 [April 2005], 295–320.)
The number 197 has a curious property:
1 + 9 + 7 = 17
9 + 7 + 17 = 33
7 + 17 + 33 = 57
17 + 33 + 57 = 107
33 + 57 + 107 = 197
After its n digits are used to initiate this pattern, the seeding number itself turns up in the resulting sequence. This makes 197 a Keith number, named for Mike Keith, the mathematician who first remarked on this property in 1987.
Keith numbers are rare and discovered only through exhaustive search, and progress stopped for 13 years after D. Lichtblau found the 34-digit 5752090994058710841670361653731519 in August 2009. But last December, while compiling a programming assignment, Ghent University mathematician Toon Baeyens found all the 35- and 36-digit Keith numbers:
23137274755282109912063039769168142
25314398891465125143523864790391288
44715370344837755402179510861188022
47933465320021485928519060435917729
196866601633638871239614307772203156
214860400509971669129437189647933258
394684240118372710589383926683340073
763701584467955209221750616718219223
880430656963418264331749765271577784
That last entry is now the largest Keith number known.
(Thanks, Peter.)
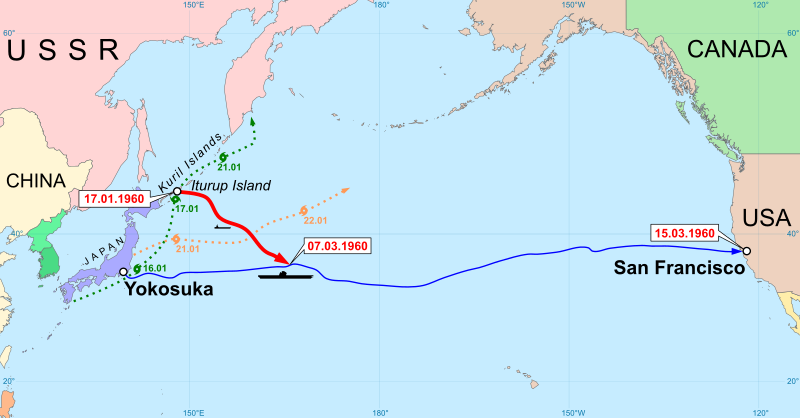
Fighting a storm in the Kuril Archipelago in January 1960, Soviet barge T-36 ran out of fuel and was carried out of its lagoon and into the open ocean. By the time the storm ceased it had also lost its radio transmitter, and when rescue crews found debris it was concluded that the vessel had sunk.
In fact it was drifting eastward across the North Pacific. The barge had recently been stocked with a three days’ supply of food and water, but some of this had been ruined in the storm, and the four-man crew were eventually reduced to eating their shoes and belts as they drifted endlessly east. “Each time we awoke, we were surprised to be alive,” private Philip Poplavski later told Time. “But we felt we were too young to die.”
Finally, after 49 days, they were spotted by an American Navy reconnaissance plane and picked up by the aircraft carrier Kearsarge. Amid worldwide publicity, the crew sailed to Paris on the Queen Mary, then flew back to the Soviet Union.

A problem by Russian mathematician Viktor Prasolov: Prove that it’s impossible to cut a 10×10 chessboard into T-shaped tiles of 4 squares each.
A digital animation by Catherine Leah Palmer.