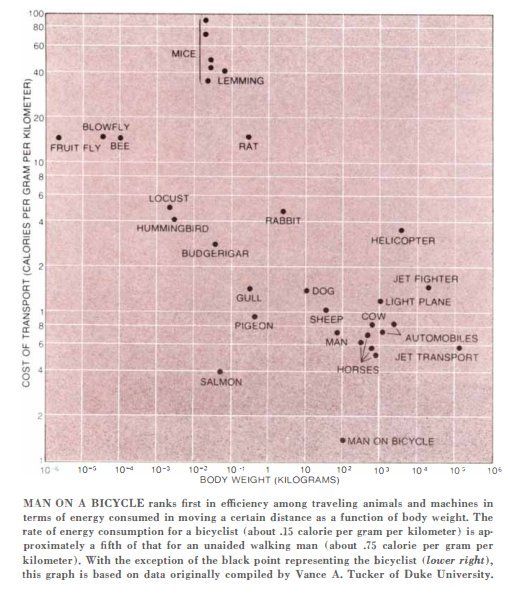
In a 1973 Scientific American article on bicycle technology, Oxford engineering lecturer S.S. Wilson showed that a man on a bicycle “improves his efficiency rating to No. 1 among moving creatures and machines”:
“When one compares the energy consumed in moving a certain distance as a function of body weight for a variety of animals and machines, one finds that an unaided walking man does fairly well (consuming about .75 calorie per gram per kilometer), but he is not as efficient as a horse, a salmon or a jet transport. With the aid of a bicycle, however, the man’s energy consumption for a given distance is reduced to about a fifth (roughly .15 calorie per gram per kilometer).”
(Via Simon Kuestenmacher’s Twitter feed.)
11/18/2018 UPDATE: In 1974 the Austrian philosopher Ivan Illich wrote:
The model American male devotes more than 1,600 hours a year to his car. He sits in it while it goes and while it stands idling. He parks it and searches for it. He earns the money to put down on it and to meet the monthly installments. He works to pay for gasoline, tolls, insurance, taxes, and tickets. He spends four of his sixteen waking hours on the road or gathering his resources for it. And this figure does not take into account the time consumed by other activities dictated by transport: time spent in hospitals, traffic courts, and garages; time spent watching automobile commercials or attending consumer education meetings to improve the quality of the next buy. The model American puts in 1,600 hours to get 7,500 miles: less than five miles per hour. In countries deprived of a transportation industry, people manage to do the same, walking wherever they want to go, and they allocate only 3 to 8 per cent of their society’s time budget to traffic instead of 28 per cent.
(Thanks, Bryan.)