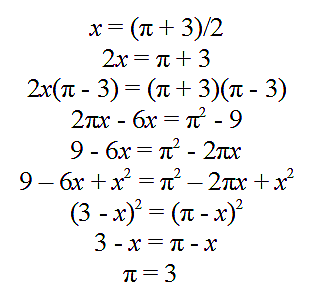
Science & Math
Math Notes
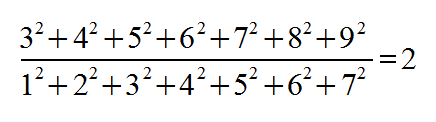
Double Duty
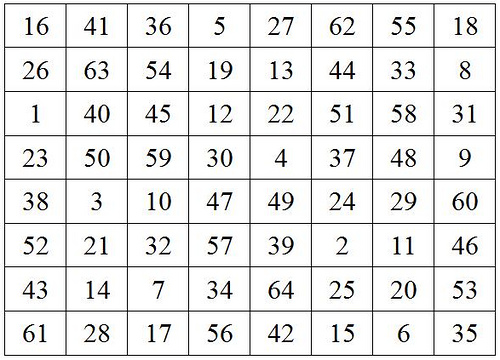
A “multi-magic” square: Each row and column sums to 260; square each term and they sum to 11,180.
Half Right
“Numero deus impare gaudet [the god delights in odd numbers].” — Virgil
“Why is it that we entertain the belief that for every purpose odd numbers are the most effectual?” — Pliny
“This is the third time; I hope good luck lies in odd numbers. … They say there is divinity in odd numbers, either in nativity, chance, or death.” — Shakespeare, The Merry Wives of Windsor
Simple Enough
Before his students arrived for a graduate course in logic, Raymond Smullyan wrote on the blackboard:
PLEASE DO NOT ERASE — BECAUSE IF YOU DO, THOSE WHO COME LATER WON’T KNOW THAT THEY SHOULDN’T ERASE.
Math Notes
Galton’s Paradox

Suppose you flip three fair coins.
Necessarily two will match, and it’s an even chance whether the third will be head or tail.
Therefore the chance that all three will match is 1/2.
Math Notes
8589934592 × 116415321826934814453125 = 1000000000000000000000000000000000
Poser
What’s the difference between six dozen dozen and half a dozen dozen?
If you answered “nothing,” reconsider.
Q.E.D.
Syllogisms offered in Lewis Carroll’s 1896 textbook in symbolic logic:
1. Babies are illogical.
2. Nobody is despised who can manage a crocodile.
3. Illogical persons are despised.
Therefore babies cannot manage crocodiles.
1. No interesting poems are unpopular among people of real taste.
2. No modern poetry is free from affectation.
3. All your poems are on the subject of soap bubbles.
4. No affected poetry is popular among people of taste.
5. Only a modern poem would be on the subject of soap bubbles.
Therefore all your poems are uninteresting.
