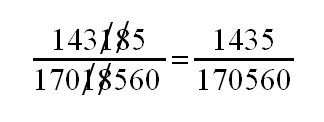
Science & Math
Start Again
THEIR ARE THREE MISTEAKS IN THIS SENTENCE.
Well, wait, there are only two. So there was a mistake of fact. Which means that the sentence really did contain three mistakes. But that means it was true all along … in which case it’s not false … in which case it really contains only two mistakes …
Arguing in Circles
Some years ago, being with a camping party in the mountains, I returned from a solitary ramble to find every one engaged in a ferocious metaphysical dispute. The corpus of the dispute was a squirrel — a live squirrel supposed to be clinging to one side of a tree-trunk; while over against the tree’s opposite side a human being was imagined to stand. This human witness tries to get sight of the squirrel by moving rapidly round the tree, but no matter how fast he goes, the squirrel moves as fast in the opposite direction, and always keeps the tree between himself and the man, so that never a glimpse of him is caught. The resultant metaphysical problem now is this: Does the man go round the squirrel or not?
— William James, Pragmatism, 1907
A Parable
Ernie and Bert are fishing. “I’ll bet you a dollar,” says Ernie, “that if you give me two dollars I’ll give you three dollars.”
Bert agrees and gives Ernie two dollars. Ernie says, “I lose,” returns one dollar and pockets the other.
Ernie goes on to found a successful software company and Bert dies a bitter alcoholic.
Concise
Here’s an achievement — in 1936 Buckminster Fuller explained Einstein’s theory of relativity in a telegram:
EINSTEIN’S FORMULA DETERMINATION INDIVIDUAL SPECIFICS RELATIVITY READS QUOTE ENERGY EQUALS MASS TIMES THE SPEED OF LIGHT SQUARED UNQUOTE SPEED OF LIGHT IDENTICAL SPEED ALL RADIATION COSMIC GAMMA X ULTRA VIOLET INFRA RED RAYS ETCETERA ONE HUNDRED EIGHTY SIX THOUSAND MILES PER SECOND WHICH SQUARED IS TOP OR PERFECT SPEED GIVING SCIENCE A FINITE VALUE FOR BASIC FACTOR IN MOTION UNIVERSE STOP SPEED OF RADIANT ENERGY BEING DIRECTIONAL OUTWARD ALL DIRECTIONS EXPANDING WAVE SURFACE DIAMETRIC POLAR SPEED AWAY FROM SELF IS TWICE SPEED IN ONE DIRECTION AND SPEED OF VOLUME INCREASE IS SQUARE OF SPEED IN ONE DIRECTION APPROXIMATELY THIRTY FIVE BILLION VOLUMETRIC MILES PER SECOND STOP FORMULA IS WRITTEN QUOTE LETTER E FOLLOWED CLOSELY BY EQUATION MARK FOLLOWED BY LETTER M FOLLOWED BY LETTER C FOLLOWED CLOSELY BY ELEVATED SMALL FIGURE TWO SYMBOL OF SQUARING UNQUOTE ONLY VARIABLE IN FORMULA IS SPECIFIC MASS SPEED IS A UNIT OF RATE WHICH IS AN INTEGRATED RATIO OF BOTH TIME AND SPACE AND NO GREATER RATE OF SPEED THAN THAT PROVIDED BY ITS CAUSE WHICH IS PURE ENERGY LATENT OR RADIANT IS ATTAINABLE STOP THE FORMULA THEREFORE PROVIDES A UNIT AND A RATE OF PERFECTION TO WHICH THE RELATIVE IMPERFECTION OF INEFFICIENCY OF ENERGY RELEASE IN RADIANT OR CONFINED DIRECTION OF ALL TEMPORAL SPACE PHENOMENA MAY BE COMPARED BY ACTUAL CALCULATION STOP SIGNIFICANCE STOP SPECIFIC QUALITY OF ANIMATES IS CONTROL WILLFUL OR OTHERWISE OF RATE AND DIRECTION ENERGY RELEASE AND APPLICATION NOT ONLY OF SELF MECHANISM BUT OF FROM SELF MACHINE DIVIDED MECHANISMS AND RELATIVITY OF ALL ANIMATES AND INANIMATES IS POTENTIAL OF ESTABLISHMENT THROUGH EINSTEIN FORMULA
The artist Isamu Noguchi was working on a commemorative sculpture in Mexico and had forgotten the precise formula E=mc2. Fuller not only described the formula but explained it — in 264 words.
04/22/2019 UPDATE: In 2009 artist Elisabetta Benassi reproduced the telegram in a carpet.
The Ladder Paradox
Imagine two men. The first is standing in a garage. The second runs into the garage carrying a ladder.
Special relativity tells us that a moving object undergoes a length contraction relative to its observer. So the man in the garage sees the ladder shorten to fit in the garage.
But the man with the ladder sees the garage shorten relative to himself — so the ladder doesn’t fit.
How is this possible?
Math Notes
45 + 15 + 55 + 05 = 4150
The Judge’s Conundrum

In the desert, a bandit shoots a sheriff. The wounded sheriff rides into town, where the outraged townspeople form a mob. They track the bandit to his desert hideout and hang him. The sheriff dies a few days later.
Now: Did the bandit kill the sheriff? If so … when and where?
Lightning Addition
A (probably apocryphal) story tells that, as a 10-year-old schoolboy, Carl Friedrich Gauss was asked to find the sum of the first 100 integers. The tyrannical schoolmaster, who had intended this task to occupy the boy for some time, was astonished when Gauss presented the correct answer, 5050, almost immediately.
How did Gauss find it?
Darkness at Noon

Solar eclipse, Aug. 11, 1999, seen from the Mir space station.
An eclipse appears total only while you’re directly in the moon’s shadow. Normally the darkness lasts only a few minutes … but in 1973 a Concorde supersonic jet managed to stay in the shade for 74 minutes.
