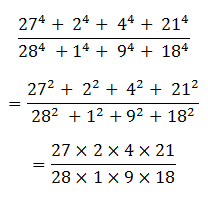You can distinguish a raw egg from a hard-boiled one by spinning it.
The reason for this was puzzled out only in 2002 by mathematicians Keith Moffat of Cambridge University and Yatuka Shimomura of Keio University. Friction between the egg and the table produces a gyroscopic effect, and the egg trades some kinetic energy for potential energy, raising its center of gravity. The raw egg can’t do this because its runny interior lags behind the shell. Moffat wrote:
Place a hard-boiled egg on a table,
And spin it as fast as you’re able;
It will stand on one end
With vectorial blend
Of precession and spin that’s quite stable.