- Mississippi didn’t ratify the 13th Amendment, abolishing slavery, until 2013.
- To protect its ecosystem, the location of Hyperion, the world’s tallest living tree, is kept secret.
- 34425 = 34 × 425
- CIRCUMSTANTIAL EVIDENCE = ACTUAL CRIME ISN’T EVINCED
- “Well, if I called the wrong number, why did you answer the phone?” — James Thurber
Science & Math
Surface Tension
Lewis Carroll on the perils of physics:
Suppose a solid held above the surface of a liquid and partially immersed: a portion of the liquid is displaced, and the level of the liquid rises. But, by this rise of level, a little bit more of the solid is of course immersed, and so there is a new displacement of a second portion of the liquid, and a consequent rise of level. Again, this second rise of level causes a yet further immersion, and by consequence another displacement of liquid and another rise. It is self-evident that this process must continue till the entire solid is immersed, and that the liquid will then begin to immerse whatever holds the solid, which, being connected with it, must for the time be considered a part of it. If you hold a stick, six feet long, with its end in a tumbler of water, and wait long enough, you must eventually be immersed. The question as to the source from which the water is supplied — which belongs to a high branch of mathematics, and is therefore beyond our present scope — does not apply to the sea. Let us therefore take the familiar instance of a man standing at the edge of the sea, at ebb-tide, with a solid in his hand, which he partially immerses: he remains steadfast and unmoved, and we all know that he must be drowned.
“The multitudes who daily perish in this manner to attest a philosophical truth, and whose bodies the unreasoning wave casts sullenly upon our thankless shores, have a truer claim to be called the martyrs of science than a Galileo or a Kepler.”
Round Trip
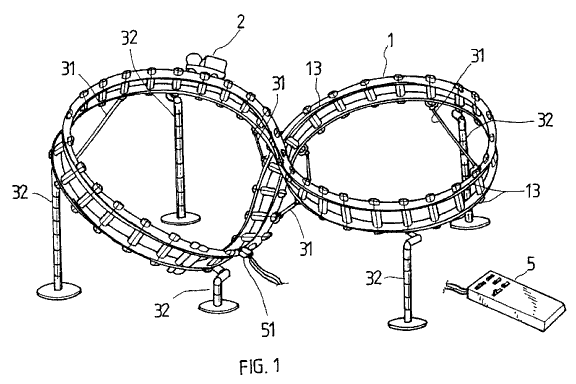
Frustrated in trying to describe higher topology abstractly to students, Xian Wang invented a model train that can hug either side of a track:
It is therefore a primary object of the present invention to provide an electrically-operated ornament travelling on a rail which can be used to explain the Mobius Theorem. … In general textbooks, this advanced mathematic rule is usually explained by demonstrating a body circularly moving on a front and a reverse side of a twisted two-ends-connected belt. Most people can not understand and imagine the theorem from such explanation and demonstration.
Of course, once you’ve built one you can put it to other uses:

Morphology

This is the opening page of “The Metamorphosis,” from Vladimir Nabokov’s teaching copy. Kafka’s novella held a special interest for Nabokov, who was a trained entomologist. From his lecture notes at Cornell:
Now, what exactly is the ‘vermin’ into which poor Gregor, the seedy commercial traveler, is so suddenly transformed? It obviously belongs to the branch of ‘jointed leggers’ (Arthropoda), to which insects, and spiders, and centipedes, and crustaceans belong. … Next question: What insect? Commentators say cockroach, which of course does not make sense. A cockroach is an insect that is flat in shape with large legs, and Gregor is anything but flat: he is convex on both sides, belly and back, and his legs are small. He approaches a cockroach in only one respect: his coloration is brown. That is all. Apart from this he has a tremendous convex belly divided into segments and a hard rounded back suggestive of wing cases. In beetles these cases conceal flimsy little wings that can be expanded and then may carry the beetle for miles and miles in a blundering flight. … Further, he has strong mandibles. He uses these organs to turn the key in a lock while standing erect on his hind legs, on his third pair of legs (a strong little pair), and this gives us the length of his body, which is about three feet long. … In the original German text the old charwoman calls him Mistkafer, a ‘dung beetle.’ It is obvious that the good woman is adding the epithet only to be friendly. He is not, technically, a dung beetle. He is merely a big beetle.
“Curiously enough,” he added, “Gregor the beetle never found out that he had wings under the hard covering of his back. This is a very nice observation on my part to be treasured all your lives. Some Gregors, some Joes and Janes, do not know that they have wings.”
Square Deal
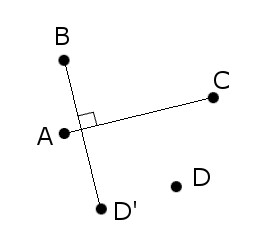
A “coffin,” or killer problem, from the oral entrance exams to the math department of Moscow State University:
Construct (with ruler and compass) a square given one point from each side.
The Shooting Room
You’re about to play a game. A single person enters a room and two dice are rolled. If the result is double sixes, he is shot. Otherwise he leaves the room and nine new players enter. Again the dice are rolled, and if the result is double sixes, all nine are shot. If not, they leave and 90 new players enter.
And so on, the number of players increasing tenfold with each round. The game continues until double sixes are rolled and a group is executed, which is certain to happen eventually. The room is infinitely large, and there’s an infinite supply of players.
If you’re selected to enter the room, how worried should you be? Not particularly: Your chance of dying is only 1 in 36.
Later your mother learns that you entered the room. How worried should she be? Extremely: About 90 percent of the people who played this game were shot.
What does your mother know that you don’t? Or vice versa?
(Paul Bartha and Christopher Hitchcock, “The Shooting Room Paradox and Conditionalizing on Measurably Challenged Sets,” Synthese, March 1999)
(Thanks, Zach.)
Pièce de Résistance
Take an ordinary magic square and replace its numbers with resistors of the same ohmic value. Now the set of resistors in each row, column, and diagonal will yield the same total resistance value when joined together end to end.
This paramagic square, by Lee Sallows, is similar — except that the resistors must be joined in parallel:

The Problem of the Two Boys
A family has two children, and you know that at least one of them is a boy. What is the probability that both are boys? There are four possibilities altogether (boy-boy, boy-girl, girl-boy, and girl-girl), and we can eliminate the last, so it would seem that the answer is 1/3.
But now suppose you visit a family that you know has two children, and that a boy comes into the room. What is the probability that both children are boys? Of the two children, you know that this one is a boy, and there is a probability of 1/2 that the other is a boy. So it seems that there is a probability of 1/2 that both are boys.
How can this be? We seem to have the same amount of information in both cases. Why does it lead us to two different conclusions?
Din Minimum
In 1958, acoustician William MacLean of the Polytechnic Institute of Brooklyn answered a perennial question: How many guests can attend a cocktail party before it becomes too noisy for conversation? He declared that the answer, for a given room, is
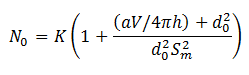
where
N0 = the critical number of guests above which each speaker will try overcome the background noise by raising his voice
K = the average number of guests in each conversational group
a = the average sound absorption coefficient of the room
V = the room’s volume
h = a properly weighted mean free path of a ray of sound
d0 = the conventional minimum distance between speakers
Sm = the minimum signal-to-noise ratio for the listeners
When the critical guest N0 arrives, each speaker is forced to increase his acoustic power in small increments (“I really don’t know what she sees in him.” — “Beg your pardon?” — “I say, I REALLY DON’T KNOW WHY SHE GOES OUT WITH HIM”) until each group is forced to huddle uncomfortably close in order to continue the conversation.
“We see therefore that, once the critical number of guests is exceeded, the party suddenly becomes a loud one,” MacLean concluded, somewhat sadly. “The power of each talker rises exponentially to a practical maximum, after which each reduces his or her talking distance below the conventional distance and then maintains, servo fashion, just the proximity, tête à tête, required to attain a workable signal-to-noise ratio. Thanks to this phenomenon the party, although a loud one, can still be confined within one apartment.”
(William R. MacLean, “On the Acoustics of Cocktail Parties,” Journal of the Acoustical Society of America, January 1959, 79-80.)
Construction Set
From the ever-inventive Lee Sallows, a self-tiling tile set:
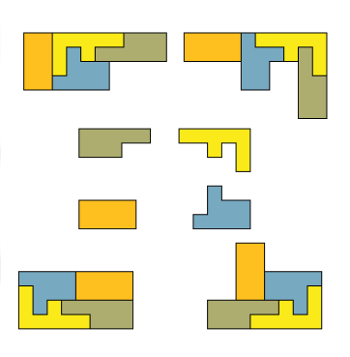
His article on such self-similar tilings appears in the December 2012 issue of Mathematics Magazine.