Black and White

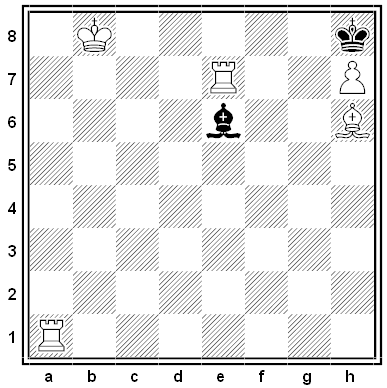
von meyenfeldt chess puzzle

A poser by F.H. von Meyenfeldt, 1967. What move must Black play to enable a forced mate in two by White?

	Select Click for Answer
… Bh3 enables 1. Rh1, and Black can’t stop 2. Bg7#. From Stephen Addison, The Book of Extraordinary Chess Problems, 1989. (10/12/2015 This seems to be cooked. After … Bg4, … Bd7, or Bc8, White can withdraw his bishop along c1-h6 and mate on the long diagonal. Thanks, Malcolm.)

October 11, 2015October 18, 2015 | Puzzles

Remainders

Some geometric legerdemain by Argentine magician Norberto Jansenson. (Thanks, Ron.)

Shifting Gears

A puzzle by French puzzle maven Pierre Berloquin:

Timothy rides a bicycle on a road that has four parts of equal length.

The first fourth is level, and he pedals at 10 kph.

The second fourth is uphill, and he pedals at 5 kph.

The third fourth is downhill, and he rides at 30 kph.

The fourth fourth is level again, but he has the wind at his back, so he goes 15 kph.

What is his average speed?

	Select Click for Answer
Let L be the length in kilometers of each fourth of the road. Then Timothy covers the first fourth in L/10 hours, the second fourth in L/5 hours, the third fourth in L/30 hours, and the fourth fourth in L/15 hours. The total time is L/10 + L/5 + L/30 + L/15 = 2L/5. Since speed equals distance divided by time, we can get Timothy’s average speed by dividing the length of the whole road, 4L, by the total time: $4L \div \displaystyle\frac{2L}{5} = 10\: \mathrm{kph}$

Click for Answer

October 8, 2015October 18, 2015 | Puzzles

Cruel and Unusual

A king is angry at two mathematicians, so he decrees the following punishment. The mathematicians will be imprisoned in towers at opposite ends of the kingdom. Each morning, a guard at each tower will flip a coin and show the result to his prisoner. Each prisoner must then guess the result of the coin flip at the other tower. If at least one of the two guesses is correct, they will live another day. But as soon as both guesses are incorrect, they will be executed.

On the way out of the throne room, the mathematicians manage to confer briefly, and they come up with a plan that will spare them indefinitely. What is it?

	Select Click for Answer
They agree that Mathematician A will always guess the result of his own flip, and Mathematician B will always guess the opposite of his own flip. This guarantees that at least one guess will always be correct. (From Max Schireson’s blog.) (Thanks, Arianna.)

October 1, 2015October 11, 2015 | Puzzles

Wanted

Items requested in the 2000 Baylor College Linguistic Scavenger Hunt:

the word for “cheese” in Estonian
the longest word in English that uses no letter more than once
a nine-letter English word that has only one syllable
the sound that a dog makes in Swedish
the regional word for “drinking fountain” that’s used in Wisconsin
the language that Jesus spoke
the American equivalent of the British word “ex-directory”
five words that are legal plays in Scrabble and that have only two letters, one of which is “x”
the motto of the Klingon Language Institute
identity of the person who said, “England and America are two countries divided by a common language.”

	Select Click for Answer
juust uncopyrightable [also dermatoglyphics] strengths or screeched vov vov bubbler Aramaic unlisted (phone number) ax, ex, xi, ox, xu “Language opens worlds.” George Bernard Shaw There’s more in the Winter 2000 issue of Verbatim (page 12).

September 28, 2015October 11, 2015 | Language · Puzzles

Black and White

kraemer chess problem

By Adolf Kraemer. White to mate in two moves.

	Select Click for Answer
1. Rc8! Kxg3 2. Qc7# From Deutsche Tageszeitung, 1922.

September 25, 2015October 4, 2015 | Puzzles

Getting More Fiber

You’re locked on the roof of a building that’s 800 feet tall, and you want to reach the ground uninjured. You can safely fall only about 5 feet. The walls of the building are completely smooth and featureless, except that one wall has a small ledge that’s 400 feet above the ground. There’s a hook on this ledge, and another hook directly above it at the edge of the roof.

You have 600 feet of rope and a knife. How can you reach the ground?

	Select Click for Answer
Cut the rope into lengths of 400 and 200 feet. You can do this by simply folding it into thirds or by measuring it against the building (tie one end to the top hook, climb down 400 feet to the ledge, cut the rope at that point, and climb back up). Now tie a loop in one end of the 200-foot rope. Pass the 400-foot rope through this loop so that half its length lies on either side. Tie the other end of the 200-foot rope to the top hook. The compound rope is 400 feet long, which is long enough to reach the ledge. Once you’re there, pull the 400-foot rope through the loop, tie it to the lower hook, and descend to the ground. That’s from Puzzling Stack Exchange. See “Stealing the Bell Ropes.”

Click for Answer

September 18, 2015September 27, 2015 | Puzzles

Heart and Head

Just offering this as a curiosity:

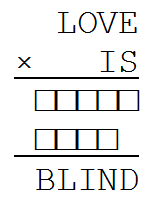
ohnishi cryptarithm

It was devised by the late Japanese cryptogramist Kyoko Ohnishi, and praised by puzzle maven Nob Yoshigahara. If each letter stands for a unique digit, what product is encoded here?

When this appeared in MIT Technology Review in November 2012, it attracted 20 responses, but it appears that all of them used computers to find the solution. If there’s a way to reason it out, I don’t think anyone has found it yet.

If we assume that neither of the factors has a leading zero, and that the partial products have five and four digits, as shown, then the solution is unique. I’ll put it in the spoiler box below, in case you want to work on it yourself.

	Select Click for Answer
The intended solution seems to be 1572 × 39 = 61308. If we allow a four-digit number as the first partial product, then 3598 × 12 = 43176 also works. Yoshigahara himself passed away in 2004, so if this has a deductive solution, I’m not sure anyone knows what it is! The problem appeared in Allan Gottlieb’s Puzzle Corner in the November/December 2012 issue of the Review, the solution in the March/April 2013 issue.

Click for Answer

September 14, 2015September 27, 2015 | Puzzles

Black and White

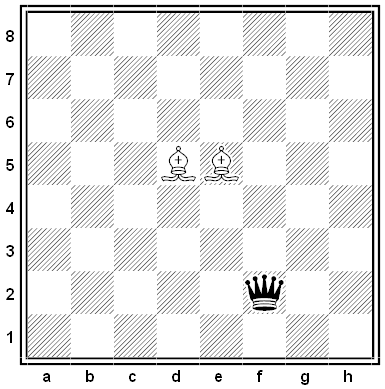
techritz problem

By M. Techritz. Place the black and white kings on the board so that White can mate in one move.

	Select Click for Answer
Place the black king on h1 and the white king on f3: Now 1. Kxf2 is mate.

September 12, 2015September 20, 2015 | Puzzles

In a Word

ditation
n. enrichment

improficuous
adj. unprofitable

Another puzzle by Yakov Perelman:

“Two fathers gave their two sons some money. One gave his son 150 rubles and the other 100 rubles. When the two sons counted their finances, they found that together they had become richer by only 150 rubles. What is the explanation?”

	Select Click for Answer
“The whole trick is that one of the fathers is the son of the other father. There are only three persons in this problem and not 4: grandfather, father and son. Grandfather gave his son 150 rubles and the latter passed on 100 of them to the grandson (i.e. his son), thus increasing his own capital by 50 rubles.” From Figures for Fun, 1957.

September 9, 2015September 20, 2015 | Language · Puzzles