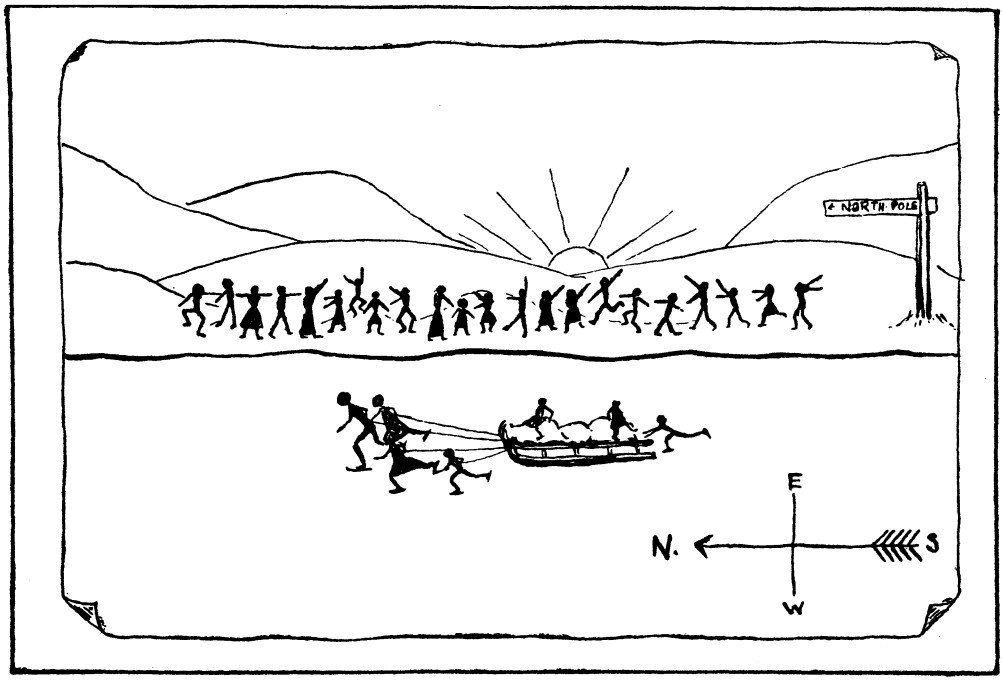
In Arthur Ransome’s 1933 children’s novel Winter Holiday, Nancy Blackett, quarantined with mumps, sends a picture to her friends of a sledge being drawn by skating figures. Nancy is encouraging the group to pursue their plan to explore a frozen lake. The seven figures in the picture correspond to the seven children in the group. “But,” asks Peggy, “what did she put in the crowd for?”
Puzzles
Saving Santa

Mathematician Matthew Scroggs’ 2025 advent calendar offers 24 puzzles, each of which has a three-digit answer. The answers will help you order the parts that Santa needs to rebuild his sleigh and save Christmas.
A new puzzle is revealed each day. Prizes will be awarded to 10 entrants who successfully build a sleigh before the end of the year. Details are here.
Progress
In 2012 I mentioned that Helen Fouché Gaines’ 1956 textbook Cryptanalysis: A Study of Ciphers and Their Solution ends with a cipher that’s never been solved. Reader Michel Esteban writes:
I think I found what kind of cipher Helen Fouché Gaines’ last challenge is.
In my opinion, it is a seriated Playfair of period 5 with two peculiarities:
– Zs are nulls in the ciphertext,
– Z is the omitted letter in the cipher square (instead of J).
If I am right, period 5 is the most likely reasonable period: we can observe no coincidences between upper and lower letters.
On the other hand, six reciprocal digrams appear: FD-DF, EC-CE, JN-NJ, JB-BJ, QL-LQ and GW-WG. These are almost certainly cipher counterparts of common reciprocal digrams (ES-SE, EN-NE, IT-TI, etc.).
I did not solve this cipher, because it is too short to use statistics. The only way to solve it is to use some metaheuristics (like Hill Climbing), but I have no computer!
I have no doubt you know someone that will be able to unveil the plaintext after having read these considerations.
Can someone help? I’ll add any updates here.
The Roving Wazir

A wazir is a fanciful chess piece that can move one square horizontally or vertically, but not diagonally. This one finds itself in the upper left corner of the board. Can it make its way to the lower right while visiting each square exactly once?
Query
From Gerald Lynton Kaufman’s The Book of Modern Puzzles (1954):
- All DROONS are the same size and shape.
- All green SLACKENS are the same size and shape.
- Twenty DROONS just fill up a MULDRUFF.
- All WALLAXES contain green SLACKENS.
- A green SLACKEN is 10% bigger than a DROON.
- A WALLAX is smaller than a MULDRUFF.
“If all MULDRUFFS and all WALLAXES are predominantly RED throughout, what is the largest possible number of green SLACKENS in a WALLAX?”
Constitution
A sobering problem from Gerald Lynton Kaufman’s Book of Modern Puzzles, 1954:
If a GLEEPER is as long as two PLONTHS and a half-GLEEPER, and a BLAHMIE is as long as two GLEEPERS and a half-BLAHMIE, and a POOSTER is as long as two BLAHMIES and a half-POOSTER, then how many PLONTHS long is a half-POOSTER?
“It may help you to make a sketch.”
Black and White

With this problem D.W.A. Brotherton won second prize in a 1955 competition for British composers under 21. White to mate in two moves.
Character Study
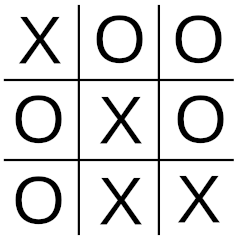
A puzzle by Paul Hoffman, from Science Digest. Could this game ever have resulted from a strict adherence to the rules of tic-tac-toe (noughts and crosses)?
Relative
A problem from Joseph Madachy’s Mathematics on Vacation (1966):
When Bert was just one year younger than Bill was when Ben was half as old as Bill will be 3 years from now, Ben was twice as old as Bill was when Ben was 1/3 as old as Bert was 3 years ago. But, when Bill was twice as old as Bert, Ben was 1/4 as old as Bill was one year ago.
“Ignoring odd months and considering that Bert has passed the half-century mark, it will be no problem to find out how old these three friends are.”
The Sands of Time
From Howard Dinesman’s Superior Mathematical Puzzles (2003):
How can you measure 9 minutes using two hourglass-style timers, one that measures 4 minutes and the other 7 minutes?