Puzzles
Cleaning House

Upend Congress and pour its members onto Constitution Avenue. Each member has up to three enemies. Prove that it’s possible to pack the 535 members back into the House and Senate in such a way that none of them has more than one enemy in his chamber. (Enmity is always mutual — I am my enemy’s enemy — and the chambers need not retain their former sizes.)
“The Ten Travelers”

Ten weary, footsore travelers,
All in a woeful plight,
Sought shelter at a wayside inn
One dark and stormy night.
“Nine beds — no more,” the landlord said,
“Have I to offer you;
To each of eight a single room,
But the ninth must serve for two.”
A din arose. The troubled host
Could only scratch his head,
For of those tired men, not two
Could occupy one bed.
The puzzled host was soon at ease —
He was a clever man —
And so to please his guests devised
This most ingenious plan.
In room marked A, two men were placed,
The third he lodged in B,
The fourth to C was then assigned —
The fifth retired to D.
In E the sixth he tucked away,
In F the seventh man;
The eighth and ninth in G and H,
And then to A he ran,
Wherein the host, as I have said,
Had laid two travelers by;
Then taking one, the tenth and last,
He lodged him safe in I.
Nine single rooms — a room for each —
Were made to serve for ten.
And this it is that puzzles me
And many wiser men.
— S.R. Ford, Ford’s Christian Repository & Home Circle, May 1888
Scandal

A puzzle from Lewis Carroll’s diary:
The Dodo says that the Hatter tells lies.
The Hatter says that the March Hare tells lies.
The March Hare says that both the Dodo and the Hatter tell lies.
Who is telling the truth?
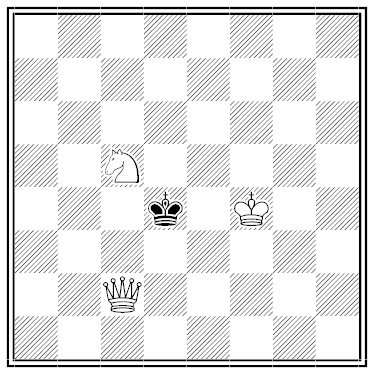
Black and White
What Are We?
A riddle by Jonathan Swift:
We are little airy creatures,
All of different voice and features:
One of us in glass is set,
One of us you’ll find in jet,
T’other you may see in tin,
And the fourth a box within;
If the fifth you should pursue,
It can never fly from you.
What are we?
Growing Pains
A problem from the Soviet Mathematical Olympiad:
Two hundred students are arranged in 10 rows of 20 children. The shortest student in each column is identified, and the tallest of these is marked A. The tallest student in each row is identified, and the shortest of these is marked B. If A and B are different people, which is taller?
Black and White
Odd and Even
Put the integers 1, 2, 3, … n in any order and call them a1, a2, a3, … an. Then form the product
P = (a1 – 1) × (a2 – 2) × (a3 – 3) … × (an – n).
Now: If n is odd, prove that P is even.
All in the Family
Two men are brothers-in-law if one is married to the other’s sister. What is the largest possible group of men in which each is brother-in-law to each of the others?