The squares of a 9×9 board are colored as shown, and then its surface is covered with 40 dominoes. Each domino covers two orthogonally adjacent squares, and the uncovered square is a black square on the boundary.
A move shifts a domino along its length by one square, so that it covers one empty square and exposes another. Prove that, for each of the black squares on the board, there’s a sequence of moves that will uncover it.
Andrzej Bartz offered these “doubly true” alphametics in the May 2017 issue of Word Ways. If the letters in each equation encode digits, what mathematical facts do these expressions represent?
CCCLVI + CCCI + CCLI = CMVIII
ONE + THIRTYNINE + NINETYONE = THREE + NINE + THIRTY + EIGHTYNINE
TWO × TWO + TEN × FIVE = SIX × NINE
anfractuous
adj. having many windings and turnings
loof
n. the palm of the hand
penetralia
n. the innermost recesses of a building
swither
n. a state of perplexity
It’s commonly said that you can defeat a hedge maze by placing one hand on a wall and carefully maintaining that contact as you advance. If the hedges are all connected, this method will reliably lead you to the center of the maze (and, indeed, to every other part of it before you return to the entrance).
The Chevening maze, in Kent, was designed deliberately to thwart this technique. Its center is concealed in an “island” of hedges distinct from the outer wall, so following either a left- or a right-hand rule will return you to the entrance without ever passing the goal.
What’s the sum of all the digits used in writing out all the numbers from one to a billion?
In a shooting match, Andryusha, Volodya, and Borya each fired 6 shots, and each totaled 71 points.
Andryusha’s first 2 shots earned him 22 points, and Volodya’s first shot earned 3 points.
Who hit the bullseye?
George Sicherman, of Sicherman dice fame, has designed a puzzle to welcome the new year: Print out the PDF, cut out the letters MMXXVI (the Roman numerals for 2026), and fit them into the tray provided so that no pieces with the same shape touch one another.
Sicherman’s website has a whole range of puzzles, most of them geometric.
(Thanks, William.)
Does the sequence of squares contain an infinite arithmetic subsequence?
A problem from the October 1964 issue of Eureka, the journal of the Cambridge University Mathematical Society:
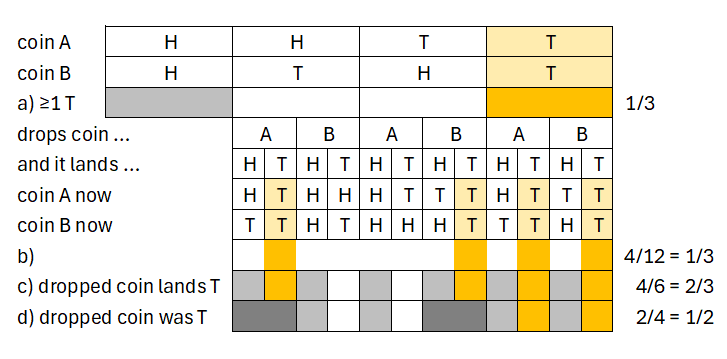
My friend tosses two coins and covers them with his hand. ‘Is there at least one “tail”?’ I ask. He affirms this (a).
Just then he accidentally knocks one of them to the floor (b). On finding the dropped coin under the table, we discover it to be a ‘tail’ (c).
‘That is all right,’ he says, ‘because it was a “tail” to start with.’ (d).
At each point (a), (b), (c) and (d) of this episode I calculated what, to the best of my knowledge, was the probability that both coins showed ‘tails’ at the time. What were these probabilities?
In a letter to Maud Standen dated Dec. 18, 1877, Lewis Carroll included a puzzle:
[M]y ‘Anagrammatic Sonnet’ will be new to you. Each line has 4 feet, and each foot is an anagram, i. e., the letters of it can be re-arranged so as to make one word. Thus there are 24 anagrams, which will occupy your leisure moments for some time, I hope. Remember, I don’t limit myself to substantives, as some do. I should consider ‘we dishwished’ a fair anagram.
As to the war, try elm. I tried.
The wig cast in, I went to ride.
‘Ring? Yes.’ We rang. ‘Let’s rap.’ We don’t.
‘O shew her wit!’ As yet she won’t.
Saw eel in Rome. Dry one: he’s wet.
I am dry. O forge! Th’rogue! Why a net?
For example, the first foot in the first line, “As to,” can be rearranged to spell OATS. Carroll left no solution, but he did add a parting riddle to which we have the answer:
“To these you may add ‘abcdefgi,’ which makes a compound word — as good a word as ‘summer-house.'” What is it?
, 
, and 
. Then 
, or (a3 – a2)(a3 + a2) = (a2 – a1)(a2 + a1). We know that (a2 + a1) < (a3 + a2), so (a2 – a1) must be greater than (a3 – a2).
is an infinite arithmetic progression. Then
