A puzzle from the 18th century — punctuate this sentence so that it makes sense:
King Charles the First walked and talked half an hour after his head was cut off.
A puzzle from the 18th century — punctuate this sentence so that it makes sense:
King Charles the First walked and talked half an hour after his head was cut off.
Punctuate this expression so that it makes sense:
Time flies you cannot they pass at such irregular intervals.
A puzzle by Virginia McCarthy:
A 20-story office building has one busy elevator. On a recent trip upward, the elevator transported seven passengers. Each of these went up at least two floors, but no two of them went up the same number of floors. On this one upward journey, no more than one passenger crossed the elevator’s threshold on any given floor; no passenger exited on the 17th floor; and the elevator’s doors opened at more odd-numbered floors than even-numbered floors. Anton was the last passenger on and the second one off. Bessie got on before Clara and after Dagwood and went up more floors than Dagwood did. Edsel went up exactly twice as many floors as Filbert and got off before Gerda got on. Gerda was not the last one to exit.
Where did each passenger enter and exit the elevator?

A “simple but pretty little puzzle” by Henry Dudeney: If this flag measures 4 feet by 3 feet and presents equal areas of red and white bunting, how wide are the cross’s arms?
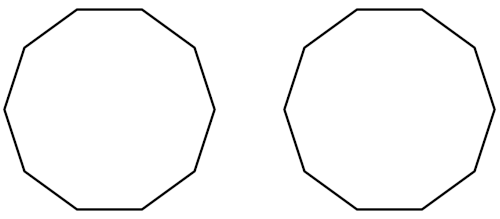
A puzzle by Russian mathematician Sergei Berlov:
Here are two decagons. Suppose that a positive integer is written at each of the 20 vertices such that the sum of the numbers around each decagon is 99. Prove that it’s possible to mark some number of successive vertices on each decagon so that the two sums of marked numbers are equal. (The marked segment on a given decagon may be a single vertex, but not all 10.)
J. Bryan III used to challenge his friends to think of an English word that contains either of the following strings of letters:
ILIL
ILIW
“I’ve never played the game with anyone who could solve either of these combinations.” Can you?
How can we make sense of this passage, composed by Willard R. Espy?
The Optic Reed has a Haste Harm. It Hose, one assumes, not to be Lever; it neither Heats the Ripple, nor Hides the Razed sinner for his Rude Rime; it is not Old. Then Leave to it; ere thy grave Loses, thou mayst find here the Hart to the Rest thou Ravest to Limb.
A circle is divided into six sectors, into which are written (say, counterclockwise) these numbers:
1, 0, 1, 0, 0, 0
You can increase any two neighboring numbers by 1. By doing this repeatedly, is there a way to make all six numbers equal?
A problem by Nikolai Rozov:
“If the brainteaser you solved before you solved this one was harder than the brainteaser you solved after you solved the brainteaser that you solved before you solved this one, was the brainteaser you solved before you solved this one harder than this one?”

By Wikimedia user Efbrazil. Fill in four squares to make a continuous dark path connecting the stars. No diagonal moves are allowed.