A puzzle by National Security Agency mathematician David B., from the agency’s October 2017 Puzzle Periodical:
Joey, the baby kangaroo has been kidnapped and placed at 2100 on a number line.
His mother, Kandice the Kangaroo, is at 0 on the number line, and will try to save him. Kandice normally jumps forward 6 units at a time. Guards have been placed at n3 on the number line, for every integer n≥1. If Kandice lands on a number with a guard on it, she will be caught and her mission will fail. Otherwise, she will safely sneak past the guard. Whenever she successfully sneaks past a guard, she gets an adrenaline rush that causes her next jump (the first jump after passing the guard) to take her 1 unit farther than it normally would (7 units instead of 6). (After a single 7-unit jump, she resumes jumping 6 units at a time, until the next time she sneaks past a guard.)
Will Kandice the Kangaroo reach (or pass) her son Joey safely?
|
SelectClick for Answer |
Yes.
First, note that two consecutive cubes are always separated by one more than a multiple of 6. To see this, note that (n+1)3 = n3 + 3n2 + 3n + 1, so (n+1)3 – n3 = 3n(n+1) + 1. n must be either even or odd; if it is even, then n(n + 1) is even, and if it is odd, then n+1 is even, so again, n(n+1) is even. Therefore, 3n(n+1) is divisible by both 2 and 3, so it must be a multiple of 6, so the difference (n+1)3 – n3 is one more than a multiple of 6.
Now, it’s easy to check that Kandice will safely jump over the first two guards (at 1 and 8). Suppose Kandice later gets caught and Gary the Guard is the first guard who catches her. Since passing the guard previous to Gary, Kandice would have finished one jump of size 7 and several jumps of size 6.
Because the distance between the guards is one more than a multiple of 6 (as shown in this illustration), counting backwards we see this pattern would have forced Kandice to land on the previous guard also. But this is impossible, since Gary was the first guard to catch Kandice. So Gary does not exist and Kandice will never be caught!
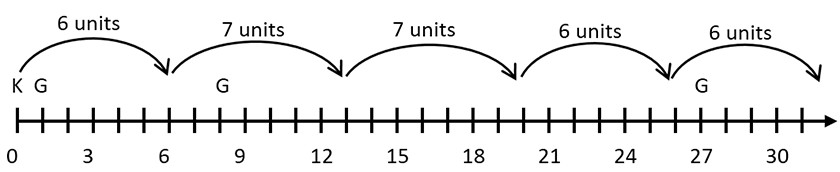
Key: Cube numbers are the positions of the guards.
Evens and odds alternate, so if some number n isn’t even, then the next number (n+1) must be even.
|