
A hybrid image by Pablo Carlos Budassi. View it from a distance.

A hybrid image by Pablo Carlos Budassi. View it from a distance.

In 2021, Istanbul’s public rail service spotted a curious passenger: “We noticed a dog using our metros and trains and he knows where to go,” spokesman Aylin Erol told India Today. “He knows where to get out. It’s like he has a purpose.”
The dog, known as Boji, is a stray Anatolian shepherd who’s been observed using the city’s buses, metro trains, trams, and ferries. Since city officials fitted him with a microchip, he’s been tracked through as many as 29 metro stations in one day, traveling up to 30 kilometers and ranging as far afield as the Princes’ Islands in the Sea of Marmara.
“You take the train and, suddenly, you see Boji,” Erol said. “And look at him. He lies, just like this. You just smile and catch the moment, really. This is what Boji evokes for Istanbulites. He also reminds us that we can still enjoy Istanbul as we rush about.”
A Weak Man going down-hill met a Strong Man going up, and said:
‘I take this direction because it requires less exertion, not from choice. I pray you, sir, assist me to regain the summit.’
‘Gladly,’ said the Strong Man, his face illuminated with the glory of his thought. ‘I have always considered my strength a sacred gift in trust for my fellow-men. I will take you up with me. Go behind me and push.’
— Ambrose Bierce, Fantastic Fables, 1899
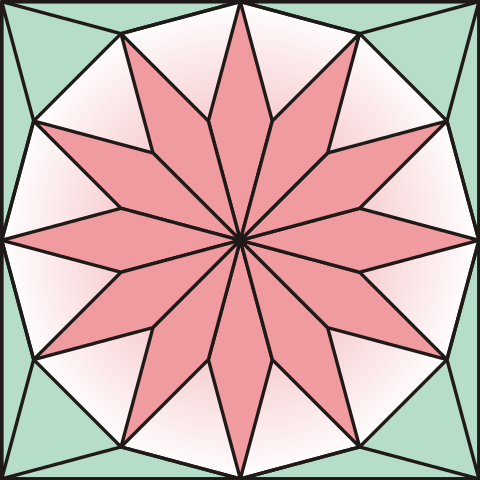
Hungarian mathematician József Kürschák offered this “proof without words” that a regular dodecagon inscribed in a unit circle has area 3. If the circle is inscribed in a square, the resulting figure can be tiled by triangles of two families — 16 equilateral triangles whose sides are equal to those of the dodecagon and 32 isosceles triangles with angles 15°-15°-150° and longest side 1. The area of the large square is 4, and the triangles that make up the dodecagon can be rearranged to fill 3 of its quadrants (see the video below). So the area of the dodecagon is 3/4 of 4, or 3.
(To see that the square and the dodecagon can be tiled as claimed, see Alexander Bogomolny’s discussion here.)
(Gerald L. Alexanderson and Kenneth Seydel, “Kürschak’s Tile,” Mathematical Gazette 62:421 [October 1978], 192-196.)
Her face Her tongue Her wit so fair so sweet so sharp first bent then drew then hit mine eye mine ear my heart Mine eye Mine ear My heart to like to learn to love her face her tongue her wit doth lead doth teach doth move Her face Her tongue Her wit with beams with sound with art doth blind doth charm doth knit mine eye mine ear my heart Mine eye Mine ear My heart with life with hope with skill her face her tongue her wit doth feed doth feast doth fill O face O tongue O wit with frowns with checks with smart wrong not vex not wound not mine eye mine ear my heart This eye This ear This heart shall joy shall yield shall swear her face her tongue her wit to serve to trust to fear.
— Arthur Gorges
“Don’t do for others what you wouldn’t think of asking them to do for you.” — Josh Billings

Released in 1978, The Campaign for North Africa has been called “the most complicated board game ever released.” On each turn a player must:
His opponent then completes the same sequence, and that constitutes just one game turn.
Reviewer Luke Winkie estimated that “If you and your group meets for three hours at a time, twice a month, you’d wrap up the campaign in about 20 years.” Reviewer Nicholas Palmer added, “No doubt the first ten years are the hardest.”
Rules of the Anti-Flirt Club, active in the early 1920s in Washington, D.C.:
The club’s main purpose was to protect women from men who abused “the precedent established during the war by offering to take young lady pedestrians in their cars,” according to an article in the Washington Post. Helen Brown, secretary of the 10-member club, warned that men “don’t all tender their invitations to save the girls a walk.”
What’s the longest possible 10-word telegram? One wordplay enthusiast offered this try, at 198 letters:
ADMINISTRATOR-GENERAL’S COUNTERREVOLUTIONARY INTERCOMMUNICATIONS UNCIRCUMSTANTIATED. QUARTERMASTER-GENERAL’S DISPROPORTIONABLENESS CHARACTERISTICALLY CONTRADISTINGUISHED UNCONSTITUTIONALISTS’ INCOMPREHENSIBILITIES.
But in Language on Vacation (1965), Dmitri Borgmann observes that “we don’t like a message interrupted by two hyphens, three apostrophes, and a period.” He offered this:
PHILOSOPHICOPSYCHOLOGICAL TRANSUBSTANTIATIONALISTS, COUNTERPROPAGANDIZING HISTORICOCABBALISTICAL FLOCCIPAUCINIHILIPILIFICATIONS ANTHROPOMORPHOLOGICALLY, UNDENOMINATIONALIZED THEOLOGICOMETAPHYSICAL ANTIDISESTABLISHMENTARIANISMS HONORIFICABILITUDINITATIBUS.
It’s 45 letters longer.
Last year Grant Maierhofer published Ebb, a novel written entirely without the letter A:
Ben went to school, worked in the Co-op, tried to write some but liked to be close with his friends. His friends comprised this kind of collective, this unity of spirit. Ben studied history. His friends studied too, some music, some writing, some science. They didn’t hope to extend their lives beyond this though, which left them odd. People who study, who hope to write, who hope to sing, who hope to push something through of their spirit, they often wish to flee, to go to New York, somewhere more, somewhere living, somewhere electric. These friends though they’d decided to let this be enough, their little communion with themselves, their communion of the work, which Ben enjoyed endlessly.
To describe the project, he wrote a thousand-word essay, itself without the letter A:
Why write the book? Good question. Possibly to try something out. To see where something brings you, then the things beyond this something. People write things. Sure, of course they do. People write things frequently. I write things, hm, since I like to figure the writing out. I bring problems on myself, then figure some route out of the box. The box? Stupid. Out of the box, outside the box? So stupid. Then how would you put it? The problem could be this cell, this thing you built surrounding your work. The problem could be the cell, then your working through it could be the tunneling out. This is nice. This is the thing, sure.
The essay and a longer excerpt are here. See The Void, The Great Gadsby, and Dead Letters.