“Knight, With Umbrella”
The difficulty with all
Forms of heroism
Is that they require
Appropriate occasions,
And that these are rarer
Even than heroes.
Counsequently, the hero
Waits and waits,
Exquisitely aware
Of the absence of any
Heroic way
To mail a letter,
Buy theatre tickets,
Or put on rubbers.
Most remarkable about
The older heroes
Is their luck in encountering
Punctual dragons,
Compliantly belligerent,
And maidens regularly
Requiring rescue.
I observe all this
A little bitterly,
Shivering
In rented armor
On an icy corner,
Late for the costume
Party, and reflecting
How long one waits,
These days,
Even for a cab.
— Elder Olson
Moonlighting

In 1788, when two thieves were arrested for robbing an Edinburgh excise office, they identified a surprising accomplice — William Brodie, a respected city councilor and president of a local trade guild.
Brodie had been leading a double life, using his day job as a cabinetmaker and locksmith to learn about residents’ security practices and to make copies of their keys, then becoming a housebreaker by night, robbing the same customers.
It appears he’d kept this up for 20 years. He was using the proceeds of the burglaries to fund a gambling career and to support five children he’d had by two different mistresses.
After the discovery he fled, but the authorities caught up to him in Amsterdam as he prepared to leave for America.
He was hanged before a crowd of 40,000 people, and his double identity helped inspire Robert Louis Stevenson to write Strange Case of Dr Jekyll and Mr Hyde.
Cause and Effect
When we are praying about the result, say, of a battle or a medical consultation, the thought will often cross our minds that (if only we knew it) the event is already decided one way or the other. I believe this to be no good reason for ceasing our prayers. The event certainly has been decided — in a sense it was decided ‘before all worlds.’ But one of the things taken into account in deciding it, and therefore one of the things that really causes it to happen, may be this very prayer that we are now offering. Thus, shocking as it may sound, I conclude that we can at noon become part causes of an event occurring at ten a.m.
— C.S. Lewis, Miracles, 1947
Lewis adds, “Some scientists would find this easier than popular thought does.” In his 2016 book Time Machine Tales, physicist Paul J. Nahin writes, “It is a view that does find much support in the block universe interpretation of Minkowskian spacetime. Lewis never mentions the block concept by name, but it is clear that he believed in the idea of God being able to see all of reality at once.” See Asking Back.
Outsider Art

This is Sunset Over the Adriatic, a painting exhibited at the 1910 Salon des Indépendants and attributed to the “excessivist” Genoan painter Joachim-Raphaël Boronali.
When critics praised the work, novelist Roland Dorgelès revealed that he’d tied a paintbrush to the tail of a donkey named Lolo to decry the excesses of modern art.
Lolo’s thoughts are not recorded.
See Different Strokes.
In a Word

argute
adj. sharp, as a taste
missment
n. a mistake, an error
mauvais quart d’heure
n. a short period of time which is embarrassing and unnerving
deligible
adj. worthy to be chosen
The label on Angostura bitters is larger than the bottle. When company founder Johann Siegert died, his sons planned to enter the tonic in a competition and divided the preparatory work between them. One oversaw the design of a new bottle, the other of a new label. They failed to coordinate the work, and by the time the mismatch was apparent they had no choice but to use the oversize labels. The oddity was so distinctive that it’s been retained as a branding measure.
(Thanks, Colin.)
Top Secret
But the most absurd and preposterous of all [ventures offered during the South Sea Bubble], and which shewed, more completely than any other, the utter madness of the people, was one started by an unknown adventurer, entitled ‘A company for carrying on an undertaking of great advantage, but nobody to know what it is.’ Were not the fact stated by scores of credible witnesses, it would be impossible to believe that any person could have been duped by such a project. The man of genius who essayed this bold and successful inroad upon public credulity, merely stated in his prospectus that the required capital was half a million, in five thousand shares of 100l. each, deposit 2l. per share. Each subscriber, paying his deposit, would be entitled to 100l. per annum per share. How this immense profit was to be obtained, he did not condescend to inform them at that time, but promised that in a month full particulars should be duly announced, and a call made for the remaining 98l. of the subscription. Next morning, at nine o’clock, this great man opened an office in Cornhill. Crowds of people beset his door, and when he shut up at three o’clock, he found that no less than one thousand shares had been subscribed for, and the deposits paid. He was thus, in five hours, the winner of 2000l. He was philosopher enough to be contented with his venture, and set off the same evening for the Continent. He was never heard of again.
— Charles Mackay, Memoirs of Extraordinary Popular Delusions and the Madness of Crowds, 1852
Eight Flights
From Lee Sallows, a geomagic square with a staircase theme:
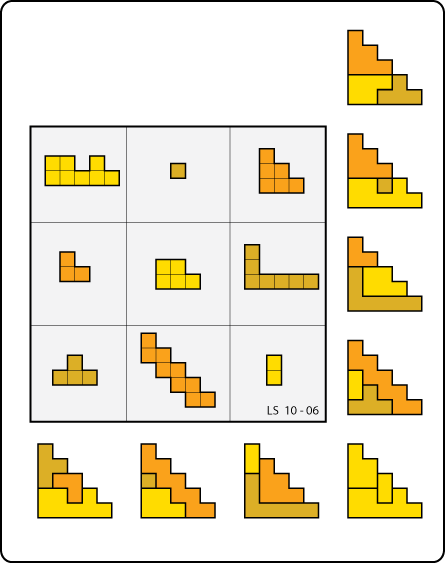
(Thanks, Lee!)
The Augsburg Book of Miracles

What is this? A mysterious illuminated manuscript seems to have appeared in Augsburg, Germany, around 1550, but no one knows who created it or for whom. The name of Augsburg printmaker Hans Burgkmair appears on one page, so he’s thought to be a contributor, but the manuscript contains no introduction, title page, table of contents, or dedication; instead it launches directly into a catalog of divine wonders and marvels of nature, each illustrated in full color.
“The manuscript is something of a prodigy in itself, it must be said,” wrote Marina Warner in the New York Review of Books in 2014. “[I]ts existence was hitherto unknown, and silence wraps its discovery; apart from the attribution to Augsburg, little is certain about the possible workshop, or the patron for whom such a splendid sequence of pictures might have been created.” Here it is.
Foremost

“If a man will be sensible and one fine morning, while he is lying in bed, count at the tips of his fingers how many things in this life truly give him enjoyment, invariably he will find food is the first one.” — Lin Yutang

