From reader Giorgos Kalogeropoulos:
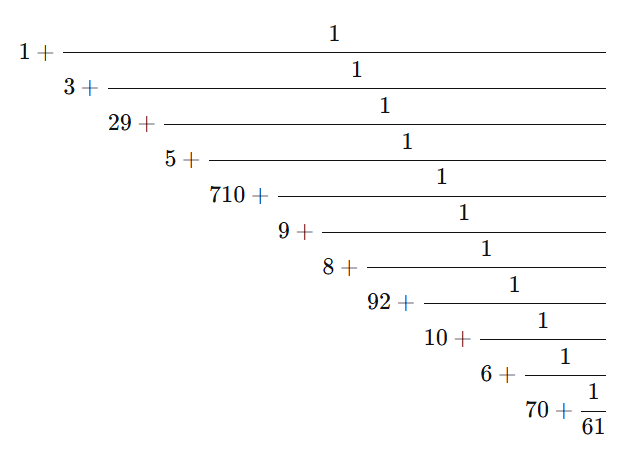
“This continued fraction converges to a constant and this constant is the terms of the continued fraction concatenated.”
Constant: 1.329571098921067061816694798131449807696979288539287861665690554139889293716015345375844973593801890…
Terms: 1, 3, 29, 5, 710, 9, 8, 92, 10, 6, 70, 61, 81, 66, 94, 7, 98, 13, 14, 4, 980, 76, 96, 97, 928, 85, 39, 2, 87, 86, 16, 65, 690, 55, 41, 398, 89, 293, 71, 60, 15, 34, 53, 75, 84, 49, 73, 59, 380, 18, 90…
“This is the lexicographically earliest sequence starting with {1,3…}.”
(Thanks, Giorgos.)