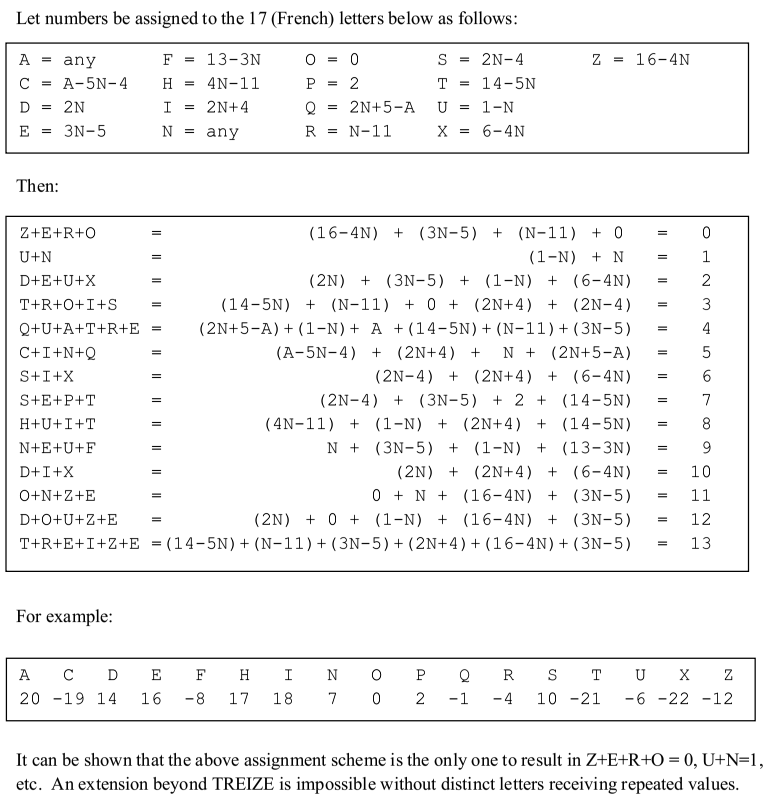
A marvelous variation on self-inventorying lists, from the inimitable Lee Sallows:
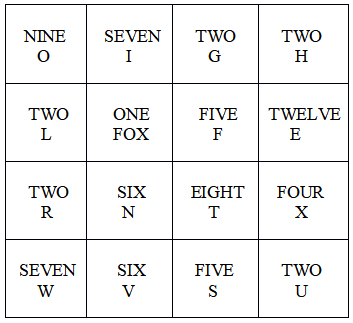
Recalling that a self-enumerating pangram corresponds to a closed loop of length 1, here follows a loop of length 2, which is to say, a pair of pangrams that enumerate each other. The pangrams are both minimal in the sense of containing none but essential letters with no “and”s or other devices openly or surreptitously added.
ONE A, ONE B, ONE C, ONE D, THIRTYONE E, FOUR F, ONE G, FIVE H, FIVE I, ONE J, ONE K, ONE L, ONE M, TWENTYTWO N, SEVENTEEN O, ONE P, ONE Q, SEVEN R, FOUR S, ELEVEN T, THREE U, FIVE V, FOUR W, ONE X, THREE Y, ONE Z.
ONE A, ONE B, ONE C, ONE D, THIRTYTWO E, SEVEN F, ONE G, FOUR H, FIVE I, ONE J, ONE K, TWO L, ONE M, TWENTY N, NINETEEN O, ONE P, ONE Q, SEVEN R, THREE S, NINE T, FOUR U, SEVEN V, THREE W, ONE X, THREE Y, ONE Z.
An alternative (non-minimal) pair includes plural s’s:
ONE A, ONE B, ONE C, ONE D, TWENTYSEVEN E’S, SIX F’S, ONE G, THREE H’S, SIX I’S, ONE L, TWENTY N’S, SIXTEEN O’S, ONE P, ONE Q, SIX R’S, NINETEEN S’S, TWELVE T’S, FOUR U’S, FOUR V’S, FIVE W’S, THREE X’S, FOUR Y’S, ONE Z.
ONE A, ONE B, ONE C, ONE D, TWENTYNINE E’S, FIVE F’S, ONE G, THREE H’S, SEVEN I’S, ONE J, ONE K, TWO L’S, ONE M, TWENTY N’S, SIXTEEN O’S, ONE P, ONE Q, SIX R’S, TWENTY S’S, TEN T’S, FOUR U’S, THREE V’S, FOUR W’S, FIVE X’S, THREE Y’S, ONE Z.
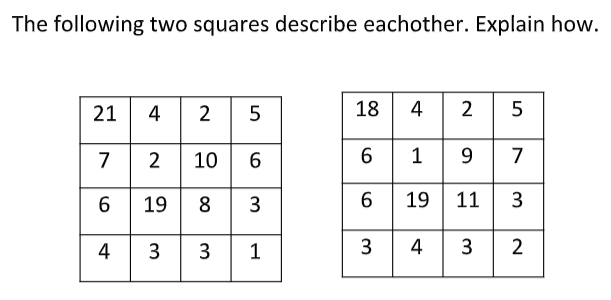
In similar vein, pangrammatic loops of length 3 follow, but now in shorthand, using arabic numerals to stand for number words, i.e. 1 = one, 2 = two, etc. The first list is enumerated by the second, the second by the third and the third by the first. The 1st loop contains minimal pangrams, the 2nd, pangrams with plural s’s:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 1 1 1 31 5 1 5 9 1 1 1 1 20 16 1 1 5 5 11 1 4 3 4 2 1
1 1 1 1 28 7 1 3 8 1 1 2 1 20 18 1 1 5 2 8 3 6 3 2 3 1
1 1 1 1 31 2 5 9 7 1 1 1 1 16 15 1 1 5 3 16 1 3 6 2 3 1
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 1 1 1 32 5 2 3 7 1 1 1 1 22 18 1 1 3 19 14 2 6 7 2 3 1
1 1 1 1 32 3 2 6 6 1 1 1 1 20 18 1 1 6 19 16 2 4 7 2 3 1
1 1 1 1 27 2 2 5 8 1 1 1 1 19 17 1 1 5 21 14 2 2 6 5 3 1
Here also a minimal pangrammatic loop of length 4 (no equivalent using plural s’s exists):
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 1 1 1 25 4 2 4 7 1 1 2 1 16 18 1 1 5 5 11 3 4 5 4 2 1
1 1 1 1 28 9 2 3 7 1 1 2 1 16 18 1 1 6 3 9 5 7 5 2 2 1
1 1 1 1 30 3 3 5 9 1 1 1 1 20 15 1 1 3 5 12 1 5 6 3 2 1
1 1 1 1 30 6 1 6 8 1 1 2 1 17 14 1 1 6 2 12 1 5 4 2 3 1
“There exist no minimal pangrammatic loops of length 5 or longer until we reach lengths 10, 33, and 55 (no plural s’s) and lengths 15, 22, 23, 207 and 312 (with plural s’s),” he adds. “This completes what I believe to be an exhaustive survey of all self-enumerating minimal pangrammatic loops.”
(Thanks, Lee.)