Next year’s date, 2025, is remarkable:
- It’s a square (452), the sum of two squares (272 + 362), the product of two squares (92 × 52), and the sum of three squares (402 + 202 + 52).
- It’s the sum of the cubes of the first nine positive integers (13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93).
- Equivalently, it’s the square of the sum of those integers (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9)2.
- It’s the second in a trio of square numbers in arithmetic progression (81, 2025, 3969).
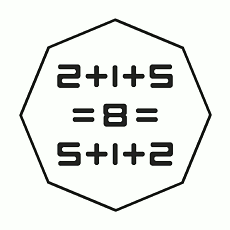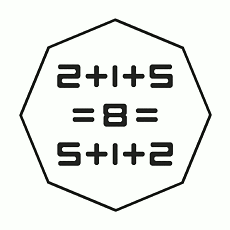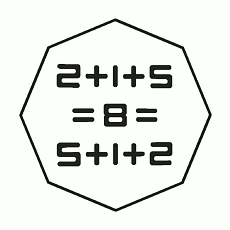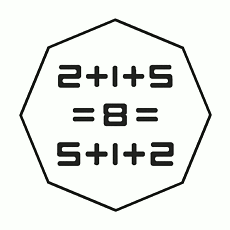
- It’s one of only three four-digit numbers whose halves can be split, summed, and squared to produce the original number: (20 + 25)2 = 2025.
- It’s the smallest square starting with 20 and the smallest number with exactly 15 odd factors (1, 3, 5, 9, 15, 25, 27, 45, 75, 81, 135, 225, 405, 675, 2025).
- It’s the sum of the entries in a 9×9 multiplication table.
- July 24, 7/24/25, will be a “Pythagorean day,” because 72 + 242 = 252.
When asked his age, Augustus De Morgan used to say, “I was x years of age in the year x2.” (He was 43 in 1849.) People born in 1980 will be able to make the same cryptic response starting next year.
(Thanks to readers Chris Smith, Sam Householder, and Jim Howell.)