“The true delight is in the finding out, rather than in the knowing.” — Isaac Asimov
A Century-Old Ghost
What does this mean?
PMVEB DWXZA XKKHQ RNFMJ VATAD YRJON FGRKD TSVWF TCRWC RLKRW ZCNBC FCONW FNOEZ QLEJB HUVLY OPFIN ZMHWC RZULG BGXLA GLZCZ GWXAH RITNW ZCQYR KFWVL CYGZE NQRNI JFEPS RWCZV TIZAQ LVEYI QVZMO RWQHL CBWZL HBPEF PROVE ZFWGZ RWLJG RANKZ ECVAW TRLBW URVSP KXWFR DOHAR RSRJJ NFJRT AXIJU RCRCP EVPGR ORAXA EFIQV QNIRV CNMTE LKHDC RXISG RGNLE RAFXO VBOBU CUXGT UEVBR ZSZSO RZIHE FVWCN OBPED ZGRAN IFIZD MFZEZ OVCJS DPRJH HVCRG IPCIF WHUKB NHKTV IVONS TNADX UNQDY PERRB PNSOR ZCLRE MLZKR YZNMN PJMQB RMJZL IKEFV CDRRN RHENC TKAXZ ESKDR GZCXD SQFGD CXSTE ZCZNI GFHGN ESUNR LYKDA AVAVX QYVEQ FMWET ZODJY RMLZJ QOBQ-
No one knows. Cryptologist Louis Kruh discovered it in the New York Public Library’s rare book room in 1993 among some old material from the U.S. Army Signal School. In 1915 first lieutenant Joseph O. Mauborgne had created what he believed was a more secure cipher than the ones currently in use, and had offered this challenge to see if his colleagues could break it. Kruh found no solution in the archive, and he published it in both The Cryptogram and Cryptologia, inviting their readers to try their hands at it. As far as I know, none succeeded.
Mauborgne described it as a “a simple, single-letter substitution cipher adapted to military use.” He invited the director of the Army Signal School to place it on a bulletin board and allow the officers there to work on it for three months and then to post the solution “to show why the standard method of attacking a substitution cipher fails in this case.” “If any attack upon this cipher is successful, I shall be glad to hear of it,” he wrote.
Kruh, who died in 2010, noted that “it was probably solved or otherwise deemed unsuitable for use because there is no knowledge of a new cipher being adopted by the Army around that time.” If a solution was found, I don’t believe anyone alive today knows what it is.
(Louis Kruh, “A 77-Year-Old Challenge Cipher,” Cryptologia 17:2 [April 1993], 172-174.)
I, Libertine

Irritated at the way bestseller lists were compiled in the 1950s, late-night radio host Jean Shepherd asked his listeners to visit bookstores and request a nonexistent book, I, Libertine, by the imaginary author Frederick R. Ewing.
The number of requests drove the title onto the New York Times bestseller list, and, encouraged by its popularity, bookstores began to order the novel. So Shepherd and publisher Ian Ballantine got novelist Theodore Sturgeon to write it, following the plot that Shepherd had described to his listeners. (Sturgeon fell asleep while trying to write the whole book in one marathon session, so Ballantine’s wife Betty had to write the last chapter.)
Ballantine Books published the novel in September 1956, using a photo of Shepherd in place of Ewing, and donated the proceeds to charity.
The Wall Street Journal exposed the hoax a few weeks before publication. “Mr. Ballantine’s idea, though simple enough, was a startling one, for publishers consider it one of the greatest possible tragedies to print a book later discovered to be the work of a literary faker,” wrote reporter Carter Henderson. “At Simon & Schuster, Inc., faces still redden when Joan Lowell’s autobiographical ‘Cradle of the Deep’ is mentioned even though this phony tale of a young girl’s spectacularly adventurous life at sea was published in 1929.”
Doing and Saying
Tim Minchin explores a key distinction.
Worldly Wisdom

Proverbs from around the world:
Every fire is the same size when it starts. — Seneca, North America
Youth is intoxication without wine; old age, wine without intoxication. — Peru
We cannot love that which we do not know. — Guinea
Second thoughts are best. — Greek
Do not propose to a girl whose home you have not seen. — Yaunde
Silence never makes mistakes. — India
Adversity makes men, prosperity monsters. — France
The threshold is the tallest mountain. — Slovenia
Punishment is a cripple, but it arrives. — Spain
Not the mouse is the thief, but the hole in the wall. — Aramaic
Praise does a wise man good but a fool harm. — Italy
A man does not seek his luck; luck seeks its man. — Turkey
He is young enough who has health, and he is rich enough who has no debts. — Denmark
God gives the wine but not the bottle. — Germany
Money likes to be counted. — Russia
Experience is a comb which nature gives us when we are bald. — China
A Word for Everything
In the 17th century natural philosopher John Wilkins set out to create a universal language for scholars, to replace Latin, whose sometimes arbitrary features made it difficult to learn. His solution, laid out in the 1668 Essay Towards a Real Character, is a system of symbols that could classify every thing and idea in the world, somewhat like the Linnaean system in biology. There are 40 main genera, each of which supplies the first two letters of a word. Each genus is divided into “differences,” which supply the next letter. And a “species” gives the fourth letter. So, for example, Zi indicates the genus “beasts,” or mammals; Zit specifies the difference “rapacious beasts of the dog kind”; and Zita gives the species “dogs.” The symbols weren’t necessarily meant to be spoken, though Wilkins later assigned phonetic values to the various characters — rather they were meant to provide an unambiguous way of classifying the world so that scholars (and, perhaps, diplomats, travelers, and merchants) could communicate clearly.
Wilkins presented the system to the Royal Society, who were impressed but concluded that it was impractical — its descriptions of similar (and confusable) items might differ by a single letter, and it would be difficult to remember all the distinctions, which seemed to invite trouble. Borges later lampooned it with his (fictional) Celestial Emporium of Benevolent Knowledge, which divides animals into 14 categories:
- Those that belong to the emperor
- Embalmed ones
- Those that are trained
- Suckling pigs
- Mermaids (or Sirens)
- Fabulous ones
- Stray dogs
- Those that are included in this classification
- Those that tremble as if they were mad
- Innumerable ones
- Those drawn with a very fine camel hair brush
- Et cetera
- Those that have just broken the flower vase
- Those that, at a distance, resemble flies
(Thanks, Alex.)
Cavalry

This is beautifully simple: The strategy game Jeson Mor, from Mongolia, is essentially a chess variant played on a 9×9 board. Each player gets nine knights, arranged as shown, and the winner is the first player who can occupy the central square and then leave that square on a subsequent turn. (Alternatively you can win by capturing all the opponent’s pieces.)
That’s it. It sounds straightforward, but with good play it becomes a delicate dance in which each side tries to prepare an attack of his own while compromising his opponent’s, and because the knights are short-range pieces, it tends to create a complex scrimmage in which an unexpected move will win the day.
You can play it online here; here’s a video of two new players trying it out.
The Seven-Spot Problem
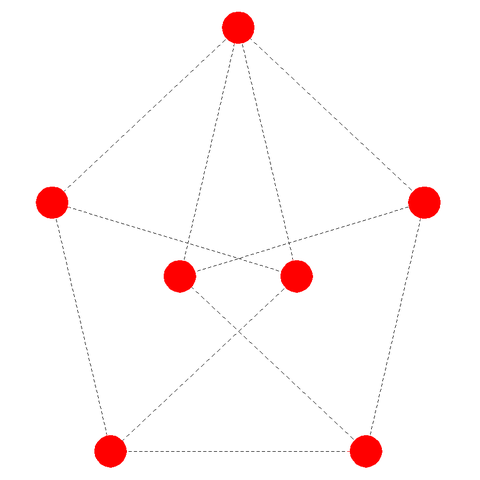
How can you arrange seven points in a plane so that if any three are chosen, at least two of them will be a unit distance apart?
The solution is shown here — it’s known as a Moser spindle.
Lightning Strikes
In 1998, the BBC reported that four card players at a whist club in Bucklesham, Suffolk, had each been dealt one suit from a shuffled deck. Hilda Golding found herself holding 13 clubs, Hazel Ruffles held 13 diamonds, and Alison Chivers held 13 hearts (and won, as this was trumps). The dummy hand, face down on the table, held 13 spades.
Though there were 55 people in the village hall at the time, some of whom claimed to have witnessed the event, it’s vastly more likely that this was some misunderstanding or a false report. In 1939 Horace Norton of University College London calculated the odds of such a deal arising naturally to be 1 in 2,235,197,406,895,366,368,301,599,999.
In The Mathematics of Games (2013), John D. Beasley writes, “A typical evening’s bridge comprises perhaps twenty deals, so a once-a-week player must play for over one hundred million years to have an even chance of receiving a thirteen-card suit. If ten million players are active once a week, a hand containing a thirteen-card suit may be expected about once every fifteen years, but it is still extremely unlikely that a genuine deal will produce four such hands.”
(Martin Gardner points out somewhere that anecdotal reports of four perfect hands are strangely more frequent than reports of two perfect hands, which is more likely — though, I guess, less newsworthy.)
(Via Martin Cohen, 101 Philosophy Problems, 2002.)
Love Triangle

Male side-blotched lizards compete for mates using a three-sided strategy that resembles a game of rock-paper-scissors. Orange-throated males, the strongest, don’t form strong pair bonds but establish large territories and fight blue-throated males outright for females. The blue-throated males, middle-sized, are less aggressive and tend to pair strongly with individual females. Yellow-throated males, the smallest, have a coloration that resembles that of females; this allows them to approach females in the territories of orange-throated males — though this won’t work with females that have formed strong pair bonds with blue-throated males.
So, broadly speaking, orange beats blue, blue beats yellow, and yellow beats orange, an equilibrium of sorts in which each variety has an advantage over another but not over the third.
