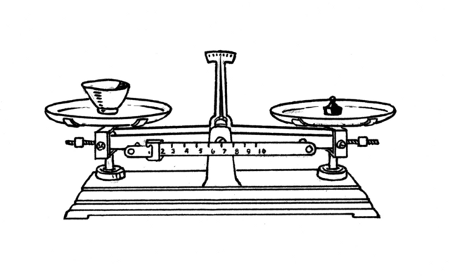
This scale balances a cup of water with a certain weight. Will the balance be upset if you put your finger in the water, if you’re careful not to touch the glass?

This scale balances a cup of water with a certain weight. Will the balance be upset if you put your finger in the water, if you’re careful not to touch the glass?

A curious puzzle by George Koltanowski, from America Salutes Comins Mansfield, 1983. “Who mates in 1?”

A puzzle by Lewis Carroll:
A bag contains one counter, known to be either white or black. A white counter is put in, the bag shaken, and a counter drawn out, which proves to be white. What is now the chance of drawing a white counter?

A puzzle by Henry Dudeney:
A lady is accustomed to buy from her greengrocer large bundles of asparagus, each twelve inches in circumference. The other day the man had no large bundles in stock, but handed her instead two small ones, each six inches in circumference. “That is the same thing,” she said, “and, of course, the price will be the same.” But the man insisted that the two bundles together contained more than the large one, and charged a few pence extra. Which was correct — the lady or the greengrocer?

Raymond Smullyan presented this puzzle on the cover of his excellent 1980 book The Chess Mysteries of Sherlock Holmes. Black moved last. What was his move?
You’ve just won a set of singles tennis. What’s the least number of times your racket can have struck the ball? Remember that if you miss the ball while serving, it’s a fault.
The Renaissance mathematician Niccolò Tartaglia would use this bewildering riddle to assess neophytes in logic:
If half of 5 were 3, what would a third of 10 be?
What’s the answer?

A mother takes two strides to her daughter’s three. If they set out walking together, each starting with the right foot, when will they first step together with the left?
A puzzle by Henry Dudeney:
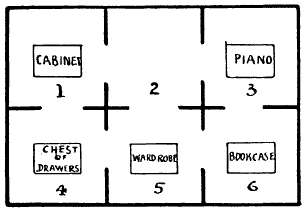
The Dobsons secured apartments at Slocomb-on-Sea. There were six rooms on the same floor, all communicating, as shown in the diagram. The rooms they took were numbers 4, 5, and 6, all facing the sea.
But a little difficulty arose. Mr. Dobson insisted that the piano and the bookcase should change rooms. This was wily, for the Dobsons were not musical, but they wanted to prevent any one else playing the instrument.
Now, the rooms were very small and the pieces of furniture indicated were very big, so that no two of these articles could be got into any room at the same time. How was the exchange to be made with the least possible labour? Suppose, for example, you first move the wardrobe into No. 2; then you can move the bookcase to No. 5 and the piano to No. 6, and so on.
It is a fascinating puzzle, but the landlady had reasons for not appreciating it. Try to solve her difficulty in the fewest possible removals with counters on a sheet of paper.