Puzzles
Half and Half
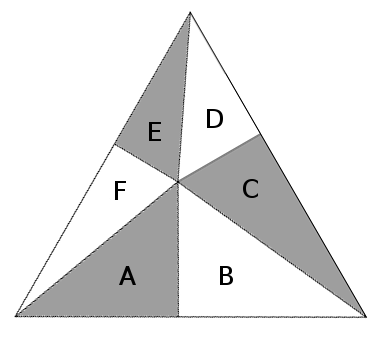
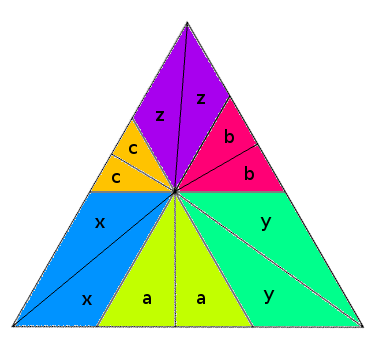
Choose an arbitrary point inside an equilateral triangle and draw segments to the vertices and perpendiculars to the sides. This divides the triangle into six smaller triangles, A, B, C, D, E, and F. Prove that the areas A + C + E and B + D + F are equal.
Black and White
Hostilities
A 10×10 chessboard contains 41 rooks. Prove that there are five rooks that don’t attack one another.
Square Deal
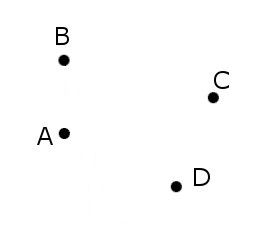
A “coffin,” or killer problem, from the oral entrance exams to the math department of Moscow State University:
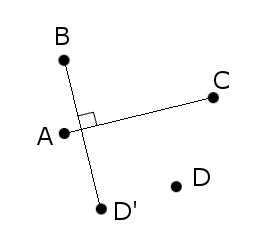
Construct (with ruler and compass) a square given one point from each side.
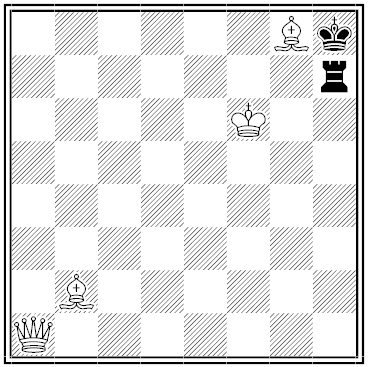
Black and White

By A.B. Arnold, from the 1859 problem tournament of the New York Clipper. White to mate in two moves.
Pigeon Puzzle
In 1982, 74-year-old David Martin found the skeleton of a carrier pigeon in the chimney of his house in Bletchingley, Surrey. Attached to its leg was an encrypted message believed to have been sent from France on D-Day, June 6, 1944:
AOAKN HVPKD FNFJW YIDDC
RQXSR DJHFP GOVFN MIAPX
PABUZ WYYNP CMPNW HJRZH
NLXKG MEMKK ONOIB AKEEQ
WAOTA RBQRH DJOFM TPZEH
LKXGH RGGHT JRZCQ FNKTQ
KLDTS FQIRW AOAKN 27 1525/6
What does it mean? No one knows — the message still hasn’t been deciphered.
“Although it is disappointing that we cannot yet read the message brought back by a brave carrier pigeon,” announced Britain’s Government Communications Headquarters last November, “it is a tribute to the skills of the wartime code makers that, despite working under severe pressure, they devised a code that was undecipherable both then and now.”
UPDATE: Gord Young of Peterborough, Ontario, claimed to have cracked the code last month using a World War I code book that he had inherited from his great-uncle. He believes the report was written by 27-year-old Lancashire Fusilier William Stott, who had been dropped into Normandy to report on German positions. Stott was killed a few weeks after the report. Here’s Young’s solution:
AOAKN – Artillery Observer At “K” Sector, Normandy
HVPKD – Have Panzers Know Directions
FNFJW – Final Note [confirming] Found Jerry’s Whereabouts
DJHFP – Determined Jerry’s Headquarters Front Posts
CMPNW – Counter Measures [against] Panzers Not Working
PABLIZ – Panzer Attack – Blitz
KLDTS – Know [where] Local Dispatch Station
27 / 1526 / 6 – June 27th, 1526 hours
Young says that the portions that remain undeciphered may have been inserted deliberately in order to confuse Germans who intercepted the message. “We stand by our statement of 22 November 2012 that without access to the relevant codebooks and details of any additional encryption used, the message will remain impossible to decrypt,” a GCHQ spokesman told the BBC on Dec. 16. But he said they would be happy to look at Young’s proposed solution.
(Thanks, John and Ivan.)
The Chelsea Pensioners
Another puzzle by Lewis Carroll:
In a group of soldiers, if 70 percent have lost an eye, 75 percent an ear, 80 percent an arm, 85 percent a leg, what percentage, at least, must have lost all four?
Black and White
Project Management

A puzzle by Polish mathematician Paul Vaderlind:
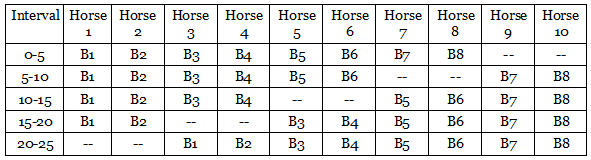
If a blacksmith requires five minutes to put on a horseshoe, can eight blacksmiths shoe 10 horses in less than half an hour? The catch: A horse can stand on three legs, but not on two.