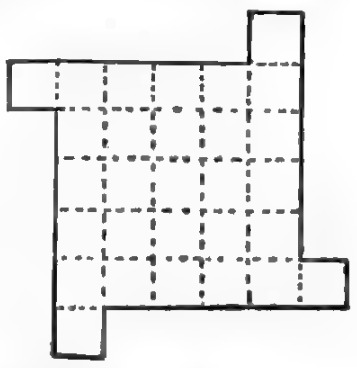
“It often happens that the easiest dissection puzzles are the prettiest,” wrote Henry Dudeney in 1914. “Here is a new one that ought to give the reader very little trouble. Cut the figure into five pieces that will fit together and form a square.”

“It often happens that the easiest dissection puzzles are the prettiest,” wrote Henry Dudeney in 1914. “Here is a new one that ought to give the reader very little trouble. Cut the figure into five pieces that will fit together and form a square.”

A puzzle by Polish mathematician Paul Vaderlind:
Is it possible to arrange 25 whole numbers (not necessarily all different) so that the sum of any three successive terms is even but the sum of all 25 is odd?
A little kingdom contains 66 people, a king and 65 citizens. Each of them, including the king, has a salary of one gold piece. When democracy comes, the king is denied a vote, but he has the power to suggest changes, in particular regarding the redistribution of salaries. The salaries must total 66, and each salary must be a whole number of gold pieces. The citizens will vote on each suggestion, which will pass if more citizens vote for it than against it. Each voter will reliably support a measure if it will increase his salary, oppose it if it will decrease his salary, and otherwise abstain from voting.
The king is greedy. What’s the highest salary he can arrange for himself?

Here’s a unit square. Prove that, if nine points are identified in the square’s interior, we can always find three of them that form a triangle of area 1/8 or less.
A puzzle by A. Vasin from the July-August 1993 issue of Quantum:
Two numbers are mirror numbers if each presents the digits of the other in reverse order, such as 123 and 321. Find two mirror numbers whose product is 92,565.
A puzzle by Y. Ionin, from the September/October 1990 issue of Quantum:
Three frogs occupy three vertices of a square. When one frog jumps over another, it lands beyond it at the same distance that had originally separated them. Can any frog reach the fourth vertex?
A puzzle by Steven T., a systems engineer at the National Security Agency, from the NSA’s September 2016 Puzzle Periodical:
Three athletes (and only three athletes) participate in a series of track and field events. Points are awarded for 1st, 2nd, and 3rd place in each event (the same points for each event, i.e. 1st always gets “x” points, 2nd always gets “y” points, 3rd always gets “z” points), with x > y > z > 0, and all point values being integers.
The athletes are named Adam, Bob, and Charlie.
Question: Who finished second in the 100-meter dash (and why)?
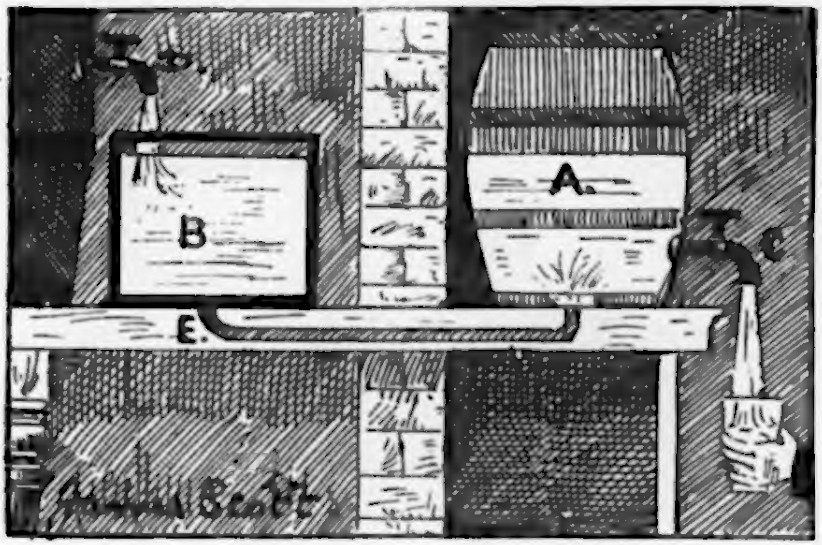
In 1895 a London shopkeeper attracted customers with a glass cask of whiskey — they were puzzled to find that no matter how much liquid they drew off, the level in the cask never dropped. The container could be viewed from any angle, and it stood well away from the wall. How was this possible?
A hidden pipe connected the bottom of the cask to a tank in another room. When a customer drew a glass of whisky, a confederate there would open a tap to replenish tank B, and the liquid, seeking its own level, would maintain the same height in the cask.
(James Scott, “Shopkeepers’ Advertising Novelties,” Strand, November 1895. See Desert Downpour.)

An old puzzle by Paul Hoffman from Science Digest. Dr. Crypton is playing chess with his boss. Crypton has the white pieces. What move can he play that will not checkmate Black? There’s no funny business; the problem is just what it seems, except that Crypton has promised never to put a knight on any square adjacent to the black king, so 1. Ne6 doesn’t count as a solution.