We learned in this problem that (spoiler!) if two squares of the same color are cut out of a chessboard, the remaining 62 squares cannot be tiled by 31 dominoes.
What if the squares removed are of different colors? Is the task possible then?
We learned in this problem that (spoiler!) if two squares of the same color are cut out of a chessboard, the remaining 62 squares cannot be tiled by 31 dominoes.
What if the squares removed are of different colors? Is the task possible then?

An anonymous puzzle from the British Chess Magazine, 1993. White to mate in half a move.
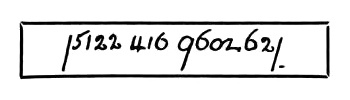
The above line of figures does not appear very interesting at first sight, but if one asks some charming member of the fair sex to turn it upside down and hold it to a mirror to read it, a hidden meaning becomes apparent.
— Strand, December 1908
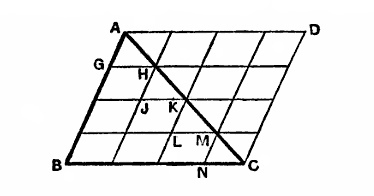
Here’s proof that one leg of a triangle always equals the sum of the other two.
ABC is our triangle. Extend it make a parallelogram, as shown, and divide the parallelogram into a grid. Obviously,
AB + BC = (AG + HJ + KL + MN) + (GH + JK + LM + NC).
Now let the grid grow increasingly fine: Instead of dividing the parallelogram into a 4×4 grid, make it 5×5, then 6×6, and so on. With each iteration, the stairstep figure described above will approximate AC more closely, and yet its total length will always equal AB + BC. Thus, at the limit, AB + BC = AC. Where is the error?
(From Henry Dudeney’s Canterbury Puzzles, via W.W. Rouse Ball’s Mathematical Recreations and Essays, 1892.)
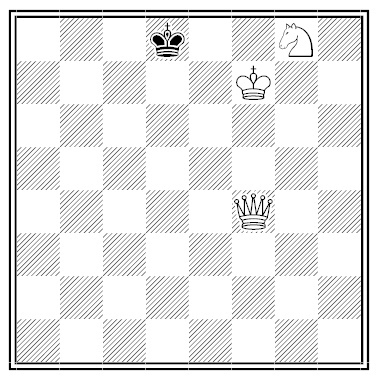
By Eric Angelini, Europe Echecs, 1990.
White adds one square at the edge of the board and then mates in two.
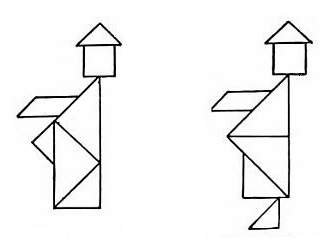
A tangram paradox by Sam Loyd. Each of these gentlemen is assembled from the same seven pieces. Yet one has a foot and the other doesn’t. How is this possible?
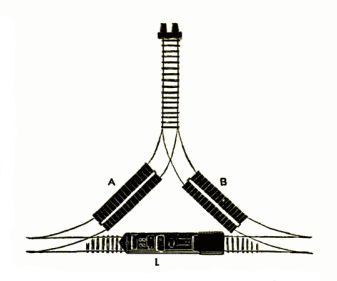
A classic railroad shunting puzzle. The segment at the top can accommodate either freight car, but not the locomotive. The freight cars can be joined if desired, and the locomotive can push or pull either or both cars from either direction. The task is to use the locomotive to swap the positions of the two cars.
From Henry Dudeney:
A better class of puzzle is the well-known one of the Railway. If New York and San Francisco are just seven days’ journey apart, and if trains start from both ends every day at noon, how many trains coming in an opposite direction will a train leaving New York meet before it arrives at its destination at San Francisco?

George Berkeley proposed that material things exist only because they are perceived to exist. In 1993, L.C. Rodó offered a suitably Berkeleyan puzzle in El Acertijo. Any piece, including a king, that is not regarded (attacked or guarded) by another piece disappears from the board. In the diagram above, every man is either attacked or guarded. But a single move (it may be by either White or Black) will set in motion a chain reaction in which all the pieces vanish from the board. What is the move?