In a 1999 quiz, the Washington Post asked its readers, “What automobile is referred to in a license plate that reads 1 DIV 0?”
The winning answer came from Supreme Court chief justice William Rehnquist, of all people. What was it?
In a 1999 quiz, the Washington Post asked its readers, “What automobile is referred to in a license plate that reads 1 DIV 0?”
The winning answer came from Supreme Court chief justice William Rehnquist, of all people. What was it?
Montana, Wyoming, and South Dakota meet at one point. Maryland, Virginia, and the District of Columbia meet at two — at Washington’s westernmost and southermost points along the Potomac River.
Name three U.S. states all three of which meet at three different points.
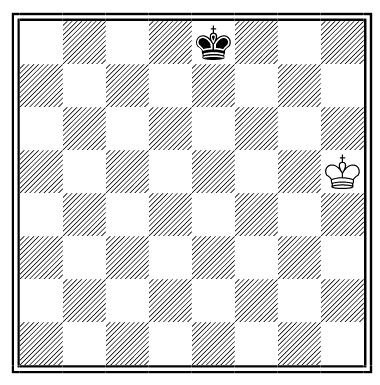
An oldie but a goodie:
From this position, White retracts his last move, then Black retracts his and replaces it with a move that permits White to mate him immediately.
You arrive in purgatory to find it’s just a typewriter on a desk. As you take your seat, you notice that the C key is glowing faintly.
A demon says, “All you have to do is type the integers, in order: ONE, TWO, and so on. The first time you strike the C key, you’ll be released into paradise.”
That doesn’t sound too bad. Assuming it takes 10 seconds on average to type each number (and that you spell each correctly, in English), how much time will pass before you first type the letter C?
You have two one-hour fuses: If you light one, it will be consumed in exactly one hour.
Unfortunately, they’re badly made — some sections of each fuse burn faster than others. You know only that each full fuse will burn in one hour.
Using only these two fuses (and matches to light them), how can you tell when 45 minutes have passed?
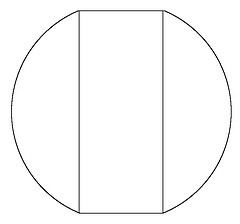
From Henry Dudeney:
A ball 13 inches in diameter has a hole 5 inches wide drilled through the center. How deep is the hole?
At a Cambridge dinner, Arthur C. Clarke asked Clive Sinclair, “What was the first human artifact to break the sound barrier?”
What was it?
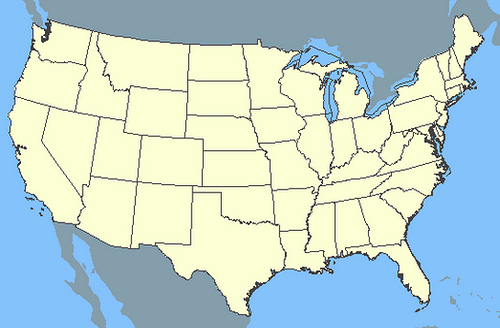
John lives in an East Coast state and Mary in a West Coast state. During a phone conversation one night, they realize that it is the same time in both locations. How can this be?
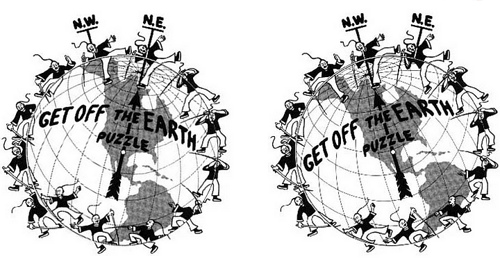
Patented in 1896, Sam Loyd’s “Get Off the Earth” puzzle reportedly sold more than 10 million copies during the puzzlemaker’s lifetime, making it one of the most popular puzzles of all time.
There are 13 men in the figure on the left. Rotating the earth produces the figure on the right — which has 12 men. What happened to the 13th man?