Puzzles
Hate Mail
In Ralph Roister Doister (1553), Ralph asks a scrivener to compose a love letter to Dame Christian Custance. But when Matthew Merrygreek reads it for her, Dame Custance is shocked to hear an insulting diatribe. This is certainly not what Ralph intended, but the scrivener confirms that he copied the letter accurately, and Merrygreek read it verbatim and in full. What’s going on here?
Sweet mistress, whereas I love you nothing at all–
Regarding your substance and richness chief of all–
For your personage, beauty, demeanour and wit,
I commend me unto you never a whit.–
Sorry to hear report of your good welfare,
For (as I hear say) such your conditions are,
That ye be worthy favour of no living man,
To be abhorred of every honest man,
To be taken for a woman inclined to vice,
Nothing at all to virtue giving her due price.–
Wherefore, concerning marriage, ye are thought
Such a fine paragon, as ne’er honest man bought.–
And now by these presents I do you advertise
That I am minded to marry you in no wise.–
For your goods and substance, I can be content
To take you as ye are. If ye mind to be my wife,
Ye shall be assured, for the time of my life,
I will keep you right well from good raiment and fare–
Ye shall not be kept but in sorrow and care–
Ye shall in no wise live at your own liberty.
Do and say what ye lust, ye shall never please me;
But when ye are merry, I will be all sad;
When ye are sorry, I will be very glad;
When ye seek your heart’s ease, I will be unkind;
At no time in me shall ye much gentleness find,
But all things contrary to your will and mind,
Shall be done–otherwise I will not be behind
To speak. And as for all them that would do you wrong,
I will so help and maintain, ye shall not live long–
Nor any foolish dolt shall cumber you but I.
I, whoe’er say nay, will stick by you till I die.
Thus, good mistress Custance, the Lord you save and keep;
From me, Roister Doister, whether I wake or sleep–
Who favoureth you no less, ye may be bold,
Than this letter purporteth, which ye have unfold.
A Little Crusade
When in Rome
What number comes next in this series?
0, 0, 0, 0, 4, 9, 5, 1, 1, 0, 55, 55, 1, 0, 1
Road Work
I set out to run a 26.5-mile marathon hoping to average less than 9 minutes per mile. As I run, my friends measure my time along various mile-long segments of the course. On each mile that they measure — indeed, on each mile that it’s possible to measure, starting anywhere along the course — my time is exactly 9 minutes. Yet my average for the whole marathon is less than 9 minutes per mile.
How is this possible?
Menagerie
How many pets do I have if all of them are dogs except two, all are cats except two, and all are fish except two?
“Four Puzzles in One”
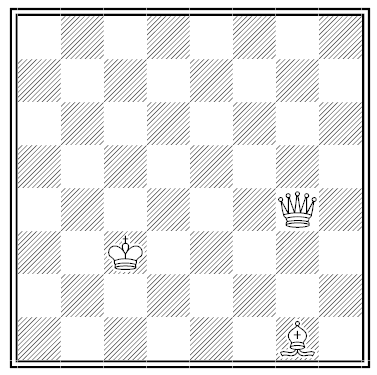
By Sam Loyd. Place the black king (a) where it can be checkmated on the move, (b) where it’s in stalemate, (c) where it’s in checkmate, and (d) where the three white pieces can’t be arranged to checkmate it.
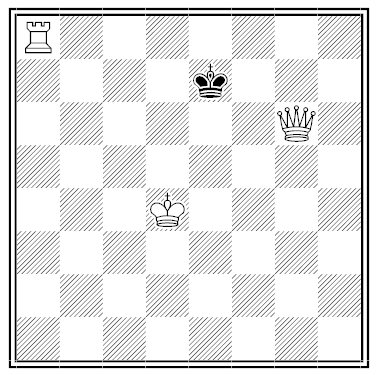
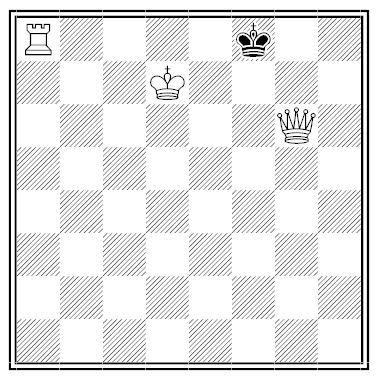
Mate in Two

By G.A.A. Walker. White to play and checkmate all six black kings simultaneously with his second move.
A Mysterious Windfall
A riddle by Isaac Newton:
Four people sat down at a table to play;
They play’d all that night, and some part of next day;
This one thing observ’d, that when all were seated,
Nobody play’d with them, and nobody betted;
Yet, when they got up, each was winner a guinea;
Who tells me this riddle I’m sure is no ninny.
Who are the players?
Erin Go
Count these leprechauns:

Now swap the two upper panels and count again:

Where has the extra one been hiding?