I loved thee, beautiful and kind,
And plighted an eternal vow;
So alter’d are thy face and mind,
‘Twere perjury to love thee now.
— Robert, Earl Nugent (1709-1788)
I loved thee, beautiful and kind,
And plighted an eternal vow;
So alter’d are thy face and mind,
‘Twere perjury to love thee now.
— Robert, Earl Nugent (1709-1788)
Has it ever occurred to you that novelists are using up experience at a dangerous rate? No, I see it hasn’t. Well, then, consider that before the novel emerged as the dominant literary form, narrative literature dealt only with the extraordinary or the allegorical — with kings and queens, giants and dragons, sublime virtue and diabolic evil. There was no risk of confusing that sort of thing with life, of course. But as soon as the novel got going, you might pick up a book at any time and read about an ordinary chap called Joe Smith doing just the sort of things you did yourself. Now, I know what you’re going to say — you’re going to say that the novelist still has to invent a lot. But that’s just the point: there’ve been such a fantastic number of novels written in the past couple of centuries that they’ve just about exhausted the possibilities of life. So all of us, you see, are really enacting events that have already been written about in some novel or other.
— David Lodge, The British Museum Is Falling Down, 1965

In the 1980s, when Nicolae Ceauşescu set about razing central Bucharest, engineer Eugeniu Iordăchescu was despairing the threat to the area’s iconic churches when he saw a waiter carrying a tray of drinks. “I saw that the secret of the glasses not falling was the tray,” he said, “so I started trying to work out how to apply a tray to the building.”
He hit on a method of digging beneath the buildings to insert reinforced concrete supports, then rolling them to new locations using hydraulic levers and mechanical pulleys. Over a period of six years, his team saved more than a dozen churches and other buildings that the Communists had planned to destroy; the 800-ton Schitul Maicilor, above, was moved almost 270 yards from its 18th-century foundations.
The technique Iordăchescu pioneered is still in use today. “He was very proud of his achievements, and even in retirement he spent a lot of time improving and helping others to push the method further on,” his son Nicholas told the New York Times. “He will be remembered for a one-of-a-kind contribution to developing this technology.”
(Thanks, Jason.)

The Feuer Buech, a 1584 treatise on munitions by Franz Helm, contains a startling illustration: a cat and a bird approaching a town, each bearing a lighted explosive.
The image accompanies a section titled “To set fire to a castle or city which you can’t get at otherwise”; Penn curator Mitch Fraas translates the relevant section:
Create a small sack like a fire-arrow … if you would like to get at a town or castle, seek to obtain a cat from that place. And bind the sack to the back of the cat, ignite it, let it glow well and thereafter let the cat go, so it runs to the nearest castle or town, and out of fear it thinks to hide itself where it ends up in barn hay or straw it will be ignited.
Fortunately it appears this was never carried into practice … though possibly birds have been used for this purpose in Russia.
rarachose
adj. rare, unusual
selcouth
adj. extraordinary in appearance
cordate
adj. heart-shaped
trothplight
n. engagement to be married
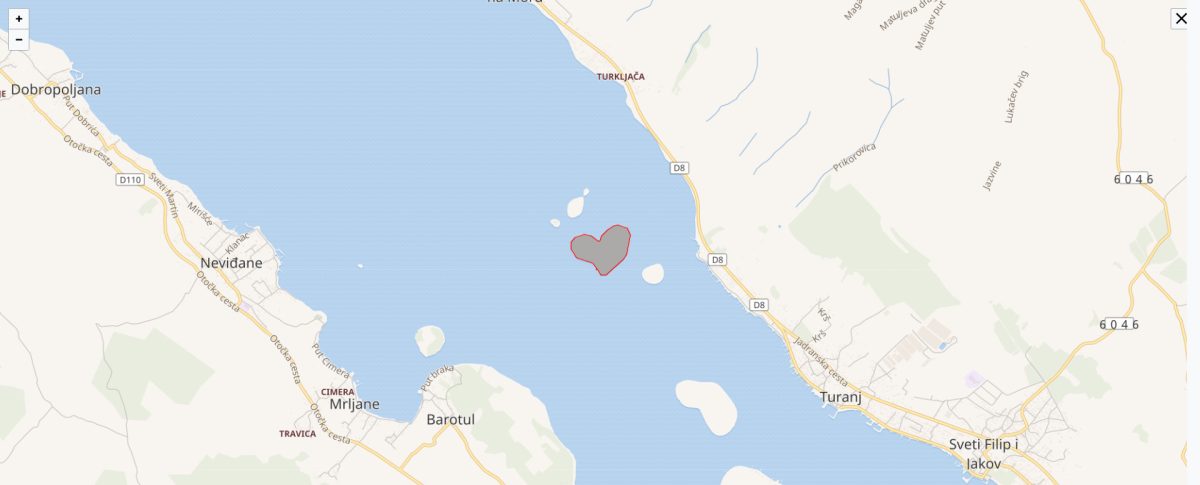
The Croatian islet Galešnjak, in the Pašman Canal of the Adriatic Sea, is one of the few naturally occurring heart-shaped objects in the world.
It’s uninhabited, but the family that owns it provides facilities for engagements and weddings.

An arrow has a 1/4 chance of hitting its target. If four arrows are shot at one target, what’s the chance that the target will be hit?

Here’s a checkerboard. Suppose we put a checker on each of the nine squares in the lower left corner. And suppose that any checker can move in any direction by jumping over an adjacent checker, provided that the square beyond it is vacant. Is there some combination of moves by which we can transfer the nine checkers to the nine squares in the upper left corner of the board?

For myself, I must say that I find [Edward] Lear funniest when he is least arbitrary and when a touch of burlesque or perverted logic makes its appearance. … While the Pobble was in the water some unidentified creatures came and ate his toes off, and when he got home his aunt remarked:
‘It’s a fact the whole world knows,
That Pobbles are happier without their toes,’which once again is funny because it has a meaning, and one might even say a political significance. For the whole theory of authoritarian governments is summed up in the statement that Pobbles were happier without their toes.
— George Orwell, “Nonsense Poetry,” 1945
An odd little item from the New Zealand Police Gazette, Sept. 20, 1893:
Christchurch. — William Strange and Co. report that between the 2nd and 4th instant their premises were broken into, and a determined but unsuccessful attempt made to break open the safe, the words ‘No time and little room; bad luck’ being written thereon with a piece of candle by the offenders. Nothing stolen.
The Strand reported that the photograph was “taken by a burglar, and subsequently sent to the makers of the safe that resisted his efforts.”
Marjory Fleming (1803-1811) composed this uniquely terrible poem at age 8:
Three Turkeys fair their last have breathed,
And now this world for ever leaved,
Their Father and their Mother too,
Will sign and weep as well as you,
Mourning for their offspring fair,
Whom they did nurse with tender care.
Indeed the rats their bones have crunch’d,
To eternity are they launch’d;
Their graceful form and pretty eyes
Their fellow fowls did not despise,
A direful death indeed they had,
That would put any parent mad,
But she was more than usual calm
She did not give a single dam.
Here ends this melancholy lay:
Farewell poor Turkeys I must say.
See Precocious and “A Sonnet on a Monkey.”