
OHIO reads the same sideways.

OHIO reads the same sideways.
Remarkable names of real people, collected in the 1980s by John Train:
Buggage had a daughter named Easter.
When James Cameron was serving as second unit director on Galaxy of Terror (1981), he was asked to film an insert of a severed arm that’s being eaten by maggots. The team made a fake arm, covered it with mealworms, lit the shot, and rolled the camera, but the mealworms didn’t move. “They looked completely inert,” Cameron said. “So I thought, well, what would happen if we put a little electrical current through these worms? Maybe they’d jump around a little more.
“So we get all ready to do the shot and two guys I knew who were producers had come up behind me to watch me work because they had heard I was doing some directing. I rolled the camera and when I said ‘Action,’ what they saw was two hundred mealworms all come to life. When I said ‘Cut,’ they stopped moving.
“This must have been tremendously impressive to two low-budget horror-movie producers. I’m sure they ratcheted up in their mind that if I could get a performance out of worms, I probably could work very well with actors.” They hired him that day to direct Piranha II.
(Robert J. Emery, The Directors: Take One, 2002.)

If your nose is close to the grindstone
And you hold it there long enough
In time you’ll say there’s no such thing
As brooks that babble and birds that sing
These three will all your world compose
Just you, the stone and your poor old nose.
— “From a two hundred-year-old stone in a country cemetery,” quoted in Christina Foyle, So Much Wisdom, 1984

Two rhapsodies on the name of French philosopher Michel Onfray, by Basile Morin.
In the chain ambigram above, the first name is transfigured (at some point) into the last.
In the tessellation ambigram below, the two names appear simultaneously as figure and ground.

From Pi Mu Epsilon Journal, November 1950:
(1/2)3 < (1/2)2.
Taking the logarithm to the base 1/2 of each member of the above inequality, we write
3 log1/2(1/2) < 2 log1/2(1/2).
But logbb = 1. Therefore
3 < 2.
Back in 2017 I wrote about the Feynman ciphers, three coded messages that had been presented as challenges to Richard Feynman in the 1950s.
Feynman couldn’t crack them, and even at the time of my post only the first of the three had been decoded — it turned out to be a transposition of the opening of Chaucer’s Canterbury Tales in Middle English. But in May 2023 David Vierra solved the other two — one turns out to be an excerpt from A.E. Housman’s 1896 poem “Terence, This is Stupid Stuff,” and the other is the start of Feynman’s 1953 paper “Atomic Theory of the λ Transition in Helium,” from The Physical Review.
Who was the “fellow scientist” who had devised these challenges? Nick Pelling thinks the most likely candidate is Paul Olum, who had been Feynman’s officemate at Los Alamos in the 1940s, but hard evidence is lacking. More at Cipher Mysteries.
(Thanks to reader Peter Dawyndt for the tip.)
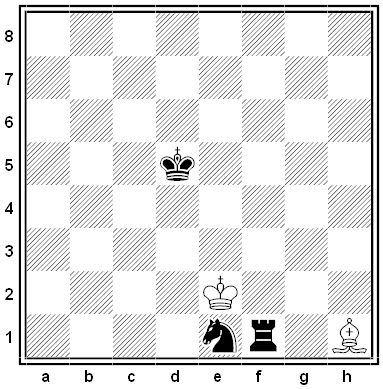
Smith College mathematician Jim Henle published this retrograde analysis puzzle in the Mathematical Intelligencer in 2018 as part of an appreciation of Raymond Smullyan. “After many moves, the chessboard appears as above. What were the last two moves?”

Several claimants have been put forth as the originators of the modern tropical cyclone ‘naming’ system. Australian weather meteorologist, Clement L. Wragge, is one of the best-established holders of the title. … Most ingeniously, he gained a measure of personal revenge by christening some of the nastiest storms with politicians’ names such as Drake, Barton, and Deakin. Modern hurricane researcher Chris Landsea noted that, by using such a personal naming system, Wragge could publicly describe a politician (say one who was less than generous with weather-bureau appropriations) as ‘causing great distress’ or ‘wandering aimlessly about the Pacific.’
— Randy Cerveny, Freaks of the Storm, 2006

In 1900, Louis Philip Perew of Tonawanda, New York, built a “gigantic man” of wood, rubber, and metal that “walks, talks, runs, jumps, [and] rolls its eyes.”
Standing 7 foot 5 in size 13 1/2 shoes and clothed in white duck, the nameless man “walked smoothly, and almost noiselessly” at an exhibition for the Strand, circling the hall twice without stopping. Perew was cagey as to its inner workings, saying only that its aluminum skin concealed a steel framework.
When a large block of wood was placed in its path, “it stopped, rolled its eyes in the direction of the obstacle, as if calculating how it could surmount it. It then deliberately raised the right foot, placed it upon the object, and stepped down on the other side. The motion seemed uncannily realistic. You almost feel like shrinking from before those rolling eyes. The visionless orbs are operated by means of clock-work situated within the head.”

When the robot announced, “I am going to walk from New York to San Francisco,” Perew acknowledged that the team planned to send it across the continent drawing a light wagon bearing two men. He claimed it could cover 20 miles in an hour.
I don’t know any more about it. This isn’t the first mechanical man we’ve encountered — a steam-powered robot had been proposed as early as 1868. But neither seems to have gone anywhere.
03/23/2025 UPDATE: Readers Kendra Colman, Justin Hilyard, and Hans Havermann point out that Cybernetic Zoo has a whole summary on the “Electric Man” and its history, including Perew’s original 1894 patent and various news articles (with additional photos) from 1895 up to 1914. Apparently the effect is deceiving — the man doesn’t actually pull the wagon, the wagon pushes the man. Many thanks to everyone who’s written in about this.