A centered hexagonal number is a number that can be represented by a hexagonal lattice with a dot in the center, like so:
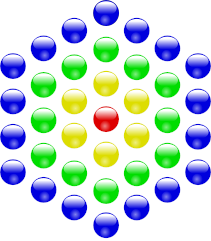
Starting at the center, successive hexagons contain 1, 7, 19, and 37 dots. The sequence goes on forever.
The sum of the first n centered hexagonal numbers is n3, and there’s a pretty “proof without words” to show that this is so:
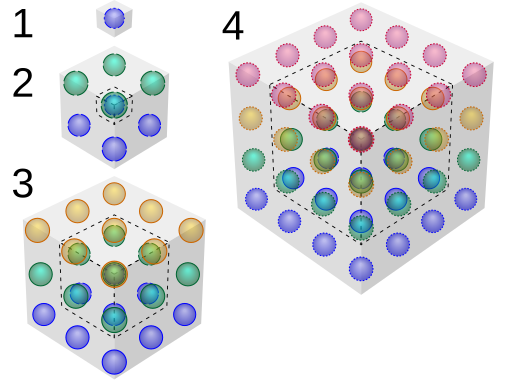
Instead of regarding each figure as a hexagon, think of it as a perspective view of a cube, looking down along a space diagonal. The first cube here contains a single dot. How many dots must we add to produce the next larger cube? Seven, and from our bird’s-eye perspective this pattern of 7 added dots matches the 7-dot hexagon shown above. The same thing happens when we advance to a 3×3×3 cube: This requires surrounding the 2×2×2 cube with 19 additional dots, and from our imagined vantage point these again take the form of a hexagonal lattice. In the last image our 33 cube must accrete another 37 dots to become a 43 cube … and the pattern continues.