“We went back to England together. When we arrived at the customs shed, Syrie said: ‘Always choose the oldest customs official. No chance of promotion.'” — Somerset Maugham, quoting his wife
Misc
- In the King James Bible, Ezra 7:21 lacks only the letter J, and 1 Chronicles 12:40 lacks only Q.
- In 2016 Pharmacy Times judged talimogene laherparepvec the hardest drug name to pronounce.
- 34 × 72 × 875 = 3472875 (B.J. van der Zwaag)
- The Estonian word kuulilennuteetunneliluuk (“bullet tunnel hatch”) is a palindrome.
- “No one ever forgets where he buried the hatchet.” — Kin Hubbard
Finger Math
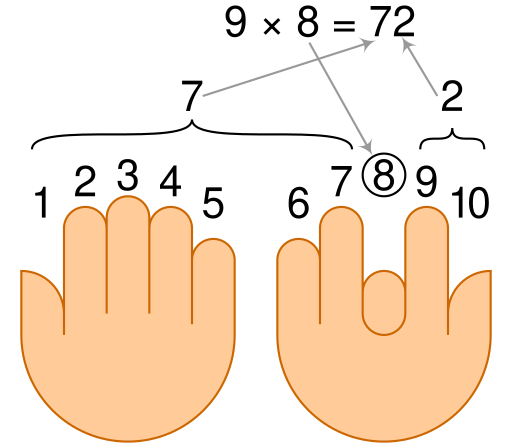
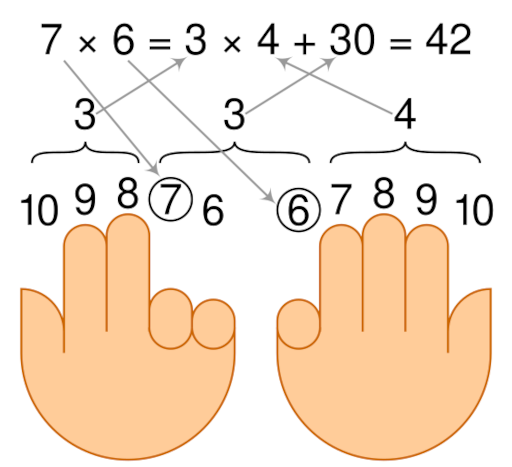
From Wikimedia user Cmglee, two digital arithmetic techniques:
Above: To multiply a positive single-digit integer by 9, hold up your hands palm up, imagine the fingers numbered consecutively 1 to 10, and fold down the finger corresponding to the number to be multiplied (here, 8). The product is the two-digit number represented by the remaining two groups of fingers — here there are seven fingers to the left of the folded finger and 2 to the right, so 9 × 8 = 72.
Below: To multiply two integers between 6 and 10, imagine each hand’s fingers numbered from 6 (pinky) to 10 (thumb), as shown. Fold down the two fingers corresponding to the factors, as well as all fingers between these two (in this example we’ll calculate 6 × 7, so fold down finger 7 on the left hand, finger 6 on the right, and the finger that lies between them, the left pinky). Count the remaining upraised fingers on the left hand (3), multiply that by the remaining upraised fingers on the right hand (4), and add 10 times the number of folded fingers (30). 3 × 4 + 30 = 42.
“Nott Shott”
A duel was lately fought in Texas by Alexander Shott and John S. Nott. Nott was shot, and Shott was not. In this case it is better to be Shott than Nott.
There was a rumor that Nott was not shot, and Shott avers that he shot Nott, which proves either that the shot Shott shot at Nott was not shot, or that Nott was shot notwithstanding.
Circumstantial evidence is not always good. It may be made to appear on trial that the shot Shott shot shot Nott, or, as accidents with fire-arms are frequent, it may be possible that the shot Shott shot shot Shott himself, when the whole affair would resolve itself into its original elements, and Shott would be shot, and Nott would not. We think, however, that the shot Shott shot shot not Shott, but Nott; anyway, it is hard to tell who was shot.
— Guy Steeley, The Modern Elocutionist or Popular Speaker, 1900
Ambiguous Latin
In Christopher Marlowe’s play Edward II, one of the king’s gaolers receives a message reading Edwardum occidere nolite timere bonum est. This can be read either as Edwardum occidere nolite; timere bonum est (“Do not kill Edward; it is good to be afraid [to do so]”) or as Edwardum occidere nolite timere; bonum est (“Do not be afraid to kill Edward; [to do so] is good”). The king is killed.
In 1213, John, Archbishop of Esztergom, was pressed to make a statement to Hungarian nobles planning the assassination of Gertrude of Merania. An assassination would have aided the church, but taking a role in it might have imperiled John’s position and his life. He wrote Reginam occidere nolite timere bonum est si omnes consentiunt ego non contradico, which also has two contradictory meanings depending on its punctuation. Reginam occidere nolite timere; bonum est; si omnes consentiunt, ego non contradico means “Do not fear to kill the queen, it is right; if everyone agrees, I do not oppose it,” but Reginam occidere nolite; timere bonum est; si omnes consentiunt, ego non; contradico means “Do not kill the queen; it is good to fear [doing so]; [even] if everyone agrees, I do not; I oppose it.” The queen, too, was murdered.
Unquote
“Stilpo having escaped the burning of his city, in which he had lost wife, children, and property, Demetrius Poliorcetes, seeing him unperturbed in expression amid the great ruin of his country, asked him if he had not suffered loss. He replied No, that thanks to God he had lost nothing of his own.” — Montaigne
“In general, the greatest reverses of fortune are the most easily borne from a sort of dignity belonging to them.” — Hazlitt
“It is easier to sacrifice great than little things.” — Montaigne
“Lessons of Noblemen”
According to the Guardian (March 1872), Lord Palmerston once dictated this sentence to 11 British cabinet ministers, “not one of whom, it is said, spelled it correctly”:
It is disagreeable to witness the embarrassment of a harassed peddler gauging the symmetry of a peeled potato.
“And Lord R. Cecil, in the House of Commons, some time ago, quoted the following lines which he said were given as a dictation exercise by an assistant commissioner to the children of a school in Ipswich”:
While hewing yew, Hugh lost his ewe,
And put it in the Hue and Cry,
To name its face’s dusky hues
Was all the effort he could use.
You brought the ewe back, by-and-by,
And only begged the hewer’s ewer,
Your hands to wash in water pure,
Lest nice-nosed ladies, not a few,
Should cry, on coming near you, “Ugh!”
Sharp Dealing
An episode from P.T. Barnum’s childhood in Bethel, Connecticut:
‘What is the price of razor strops?’ inquired my grandfather of a peddler, whose wagon, loaded with Yankee notions, stood in front of our store.
‘A dollar each for Pomeroy’s strops,’ responded the itinerant merchant.
‘A dollar apiece!’ exclaimed my grandfather; ‘they’ll be sold for half the money before the year is out.’
‘If one of Pomeroy’s strops is sold for fifty cents within a year, I’ll make you a present of one,’ replied the peddler.
‘I’ll purchase one on those conditions. Now, Ben, I call you to witness the contract,’ said my grandfather, addressing himself to Esquire Hoyt.
‘All right,’ responded Ben.
‘Yes,’ said the peddler, ‘I’ll do as I say, and there’s no backout to me.’
My grandfather took the strop, and put it in his side coat pocket.
Presently drawing it out, and turning to Esquire Hoyt, he said, ‘Ben, I don’t much like this strop now I have bought it. How much will you give for it?’
‘Well, I guess, seeing it’s you, I’ll give fifty cents,’ drawled the ‘Squire, with a wicked twinkle in his eye, which said that the strop and the peddler were both incontinently sold.
‘You can take it. I guess I’ll get along with my old one a spell longer,’ said my grandfather, giving the peddler a knowing look.
The strop changed hands, and the peddler exclaimed, ‘I acknowledge, gentlemen; what’s to pay?’
‘Treat the company, and confess you are taken in, or else give me a strop,’ replied my grandfather.
‘I never will confess nor treat,’ said the peddler, ‘but I’ll give you a strop for your wit;’ and suiting the action to the word, he handed a second strop to his customer. A hearty laugh ensued, in which the peddler joined.
‘Some pretty sharp fellows here in Bethel,’ said a bystander, addressing the peddler.
‘Tolerable, but nothing to brag of,’ replied the peddler; ‘I have made seventy-five cents by the operation.’
‘How is that?’ was the inquiry.
‘I have received a dollar for two strops which cost me only twelve and a half cents each,’ replied the peddler; ‘but having heard of the cute tricks of the Bethel chaps, I thought I would look out for them and fix my prices accordingly. I generally sell these strops at twenty-five cents each, but, gentlemen, if you want any more at fifty cents apiece, I shall be happy to supply your whole village.’
Our neighbors laughed out of the other side of their mouths, but no more strops were purchased.
(From his 1855 autobiography.)
Quickie
Punctuate this expression so that it makes sense:
Time flies you cannot they pass at such irregular intervals.
Coming and Going
If Socrates was born, Socrates became either when Socrates existed not or when Socrates already existed; but if he shall be said to have become when he already existed, he will have become twice; and if when he did not exist, Socrates was both existent and non-existent at the same time — existent through having become, non-existent by hypothesis. And if Socrates died, he died either when he lived or when he died. Now he did not die when he lived, since he would have been at once both alive and dead; nor yet when he died, since he would have been dead twice. Therefore Socrates did not die. And by applying this argument in turn to each of the things said to become or perish it is possible to abolish becoming and perishing.
— Sextus Empiricus
