What’s remarkable about this sentence, composed by Dmitri Borgmann?
IN JULY, OH MY KILLJOY MOLLY, I’LL LOOK IN UPON MY JUMPY POLO PONY UP IN HILLY HONOLULU.
What’s remarkable about this sentence, composed by Dmitri Borgmann?
IN JULY, OH MY KILLJOY MOLLY, I’LL LOOK IN UPON MY JUMPY POLO PONY UP IN HILLY HONOLULU.
Confined in Colchester Castle during the English civil war, the royalist officer Sir John Trevanion was awaiting execution when he received this letter:
Worthie Sir John:- Hope, that is ye beste comfort of ye afflicted, cannot much, I fear me, help you now. That I would saye to you, is this only: if ever I may be able to requite that I do owe you, stand not upon asking me. ‘Tis not much that I can do: but what I can do, bee ye verie sure I wille. I knowe that, if dethe comes, if ordinary men fear it, it frights not you, accounting it for a high honor, to have such a rewarde of your loyalty. Pray yet that you may be spared this soe bitter, cup. I fear not that you will grudge any sufferings; only if bie submission you can turn them away, ’tis the part of a wise man. Tell me, an if you can, to do for you anythinge that you wolde have done. The general goes back on Wednesday. Restinge your servant to command. — R.T.
Sir John studied the message for several hours, and then, apparently despairing, asked to spend some time alone in prayer. His captors agreed — and never saw him again.
Read the third letter after each punctuation mark.
Andy and Bill are traveling when they meet Carl. Andy has 5 loaves of bread and Bill has 3; Carl has none and asks to share theirs, promising to pay them 8 gold pieces when they reach the next town.
They agree and divide the bread equally among them. When they reach the next town, Carl offers 5 gold pieces to Andy and 3 to Bill.
“Excuse me,” says Andy. “That’s not equitable.” He proposes another arrangement, which, on consideration, Bill and Carl agree is correct and fair.
How do they divide the 8 gold pieces?

Henry Dudeney says this puzzle is “supposed to be Chinese, many hundreds of years old, and never fails to interest.” White to play and mate, moving each of the three pieces exactly once.

Suppose a man sets out to climb a mountain at sunrise, arriving at the top at sunset. He sleeps at the top and descends the following day, traveling somewhat more quickly downhill. Prove that there’s a point on the path that he will pass at the same time on both days.
A puzzle from Henry Dudeney’s Amusements in Mathematics (1917):
There is a certain village in Japan, situated in a very low valley, and yet the sun is nearer to the inhabitants every noon, by 3,000 miles and upwards, than when he either rises or sets to these people. In what part of the country is the village situated?
Place two white rooks and a white knight on this board so that Black is checkmated:
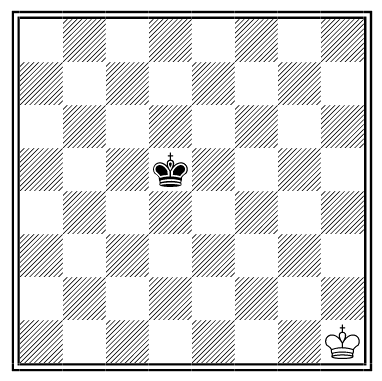
The solution need not be reachable in a normal game.
In 1735, an anonymous “lover of mathematicks” offered the following conundrum:
“‘Tis certainly Matter of Fact, that three certain Travellers went on a Journey, in which, tho’ their Heads travelled full twelve Yards more than their Feet, yet they all return’d alive, with their Heads on.”
How is this possible?
Suppose I show you two old coins. One is dated 51 B.C., and the other is marked George I. Which is authentic?
If you were a British soldier in Malta in the 19th century, you might receive this card from a local dram-shop:

What does it mean?