
LINENLESSNESSES has one I, two Ls, three Ns, four Es, and five Ss.
(Discovered by Sir Jeremy Morse.)

LINENLESSNESSES has one I, two Ls, three Ns, four Es, and five Ss.
(Discovered by Sir Jeremy Morse.)

“It is harder to make one’s name by means of a perfect work than to win praise for a second-rate one by means of the name one has already acquired.” — Jean de La Bruyère

In 1911, three British explorers made a perilous 70-mile journey in the dead of the Antarctic winter to gather eggs from a penguin rookery in McMurdo Sound. In this week’s episode of the Futility Closet podcast we’ll follow the three through perpetual darkness and bone-shattering cold on what one man called “the worst journey in the world.”
We’ll also dazzle some computers and puzzle over some patriotic highways.
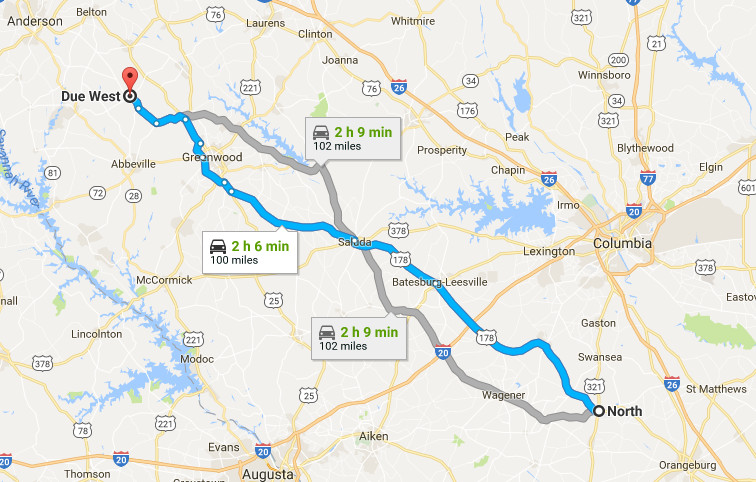
North, South Carolina, is 100 miles southeast of Due West.
Also: Northwest, North Carolina, is in southeast North Carolina, due east of Due West, South Carolina, and east and slightly north of North, South Carolina.
(Thanks, Bob and Rick.)
And while we’re at it:

Proverbs from around the world:
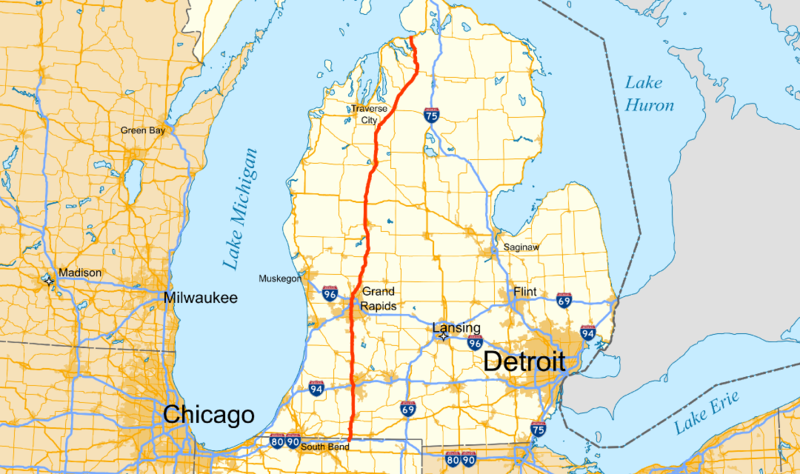
Canada is south of Detroit.
Due to a curve in the border, Windsor, Ontario, lies south of Michigan’s largest city.
A floral compass in Windsor bears a plaque that reads:
THE GEOGRAPHICAL LOCATION OF THE U.S.A. AT THIS POINT LIES DUE NORTH OF CANADA

The Spanish monk Florentius made a humble appeal to posterity in 945: Start at the F at top center, and as long as your path works steadily either southeast or southwest you’ll spell out FLORENTIUM INDIGNUM MEMORARE, “Remember unworthy Florentius.”
His manuscript is now in the Biblioteca Nacional de España, so it appears he got his wish.
This must have scared the daylights out of people in 1895 — The Execution of Mary Stuart, one of the first films to use editing for special effects.
After the executioner raises his ax, the actress is replaced with a mannequin.

“We now give what is acknowledged to be the finest two-move problem extant,” wrote J.H. Blackburne in the Strand in 1908. “It is by the American expert, W.A. Shinkman, and is also claimed by G.E. Carpenter, a fellow countryman of his. Here we have not only a difficult key-move, but also beauty of theme and artistic construction, the three essential qualities necessary to a perfect problem.”
White to mate in two moves.

abscede
v. to move away or apart; to lose contact; to separate
anachorism
n. something located in an incongruous position
longinquity
n. greatness of distance; remoteness
aerumnous
adj. troubled; distressed
In 2007 Brazilian villagers were surprised to discover a 16-foot minke whale on a sandbank in the Tapajos River, 1,000 miles from the sea. Apparently it had got separated from its group in the Atlantic and swum up the Amazon.
After two days, rescuers managed to return it to the water. “What we can definitely say is that it lost its way,” biologist Fabia Luna told Globo television. “It entered the river, which on its own is unusual. But then to have travelled around 1,500 kilometers is both strange and adverse.”
Brazil’s environmental agency said the whale might have been in the region for two months before it was spotted. “It is outside of its normal habitat, in a strange situation, under stress, and far from the ocean,” said whale expert Katia Groch. “The probability of survival is low.”