From Lee Sallows:

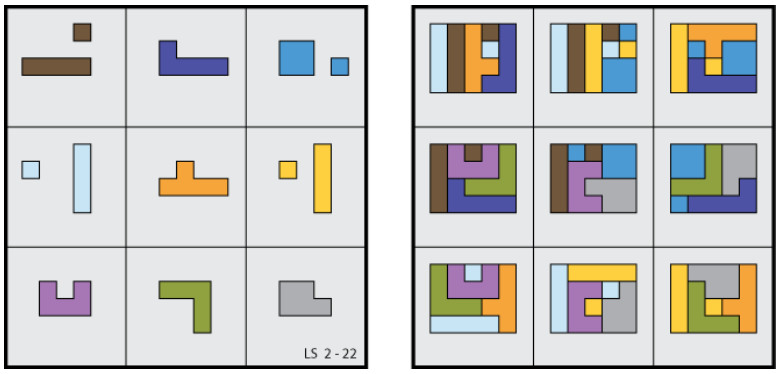
A recent contribution to Futility Closet showed an atypical type of 3×3 geometric magic square in which the 4 pieces occupying each of its nine 2×2 subsquares are able to tile the same rectangle. A different square with the same property is seen in the figure here shown, where the nine tiled rectangles appear at right.

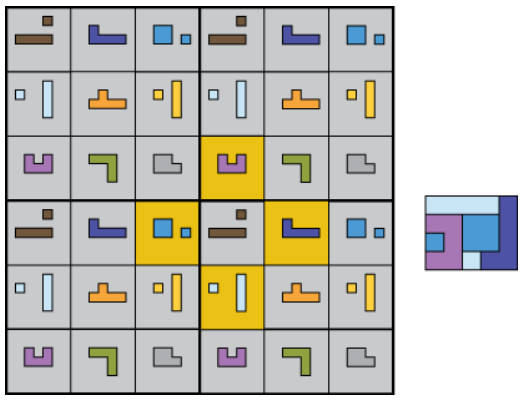
As in the earlier example, the square is to be interpreted as if drawn on a torus, the relations among its peripheral cells then being the same as those that result if the square is surrounded with copies of itself, as seen in the following figure showing four such copies, one in each quadrant:

The figure makes it easier to identify the different 2 × 2 subsquares, exactly nine distinct examples of which can be identified. A brief commentary on the square pointed out that the number of ‘magic’ conditions it satisfies is one greater than the eight conditions demanded by a conventional 3 × 3 magic square. Hence the title of the piece, ‘Extra Magic.’

It was while perusing this diagram that an alternative division of the cells into sets of 4 suggested itself. Instead of 2 × 2 subsquares, consider the four cells defined by a cross that can be centered on any chosen cell. The above figure shows a yellow-shaded example, along with a rectangle tiled by its four associated shapes. It is interesting to note that, as before, there are just nine distinct crosses of this kind to be found in a 3 × 3 square. An obvious question thereby prompted was whether or not a new 3 × 3 magic square could be found based upon such crosses rather than 2×2 subsquares? The answer turned out to be yes, but in the process of scrutinizing an initial specimen I noticed that although it embodied nine cross-based sets of 4 rectangle-tiling pieces, as required, it also included a couple of additional rectangle-tiling sets contained within 2 × 2 subsquares. Clearly the maximum number of such surplus sets would be nine, one for each cross, but could a specimen showing nine cross-based and nine subsquare-based rectangle-tiling sets really exist? I lost no time in seeking an answer.

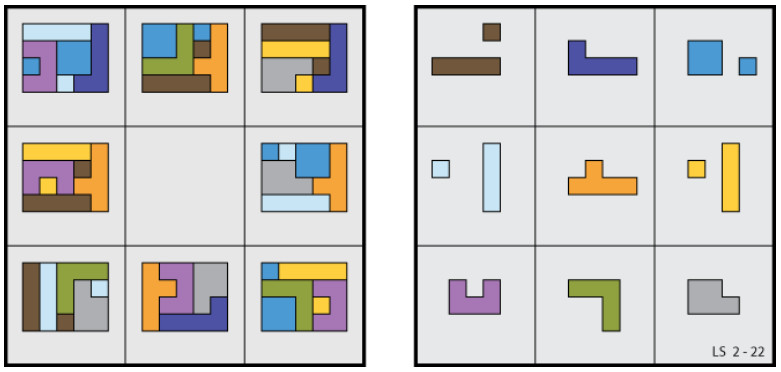
Regrettably, I was unable to find one. However, the figure below shows a close approach to perfection. It is the same 3 × 3 square with which we started, but now shown alongside no less than eight additional rectangles, each of them tiled with a set of 4 pieces belonging to a cross. Note that the missing rectangle is the one belonging to the non-magic central cross, a show of symmetry that seems appropriate.

So whereas a 3 × 3 magic square, numerical or geometric, satisfies at least 8 separate conditions (3 rows + 3 columns + 2 diagonals), the square here shown satisfies no less than eight more.

(Thanks, Lee.)