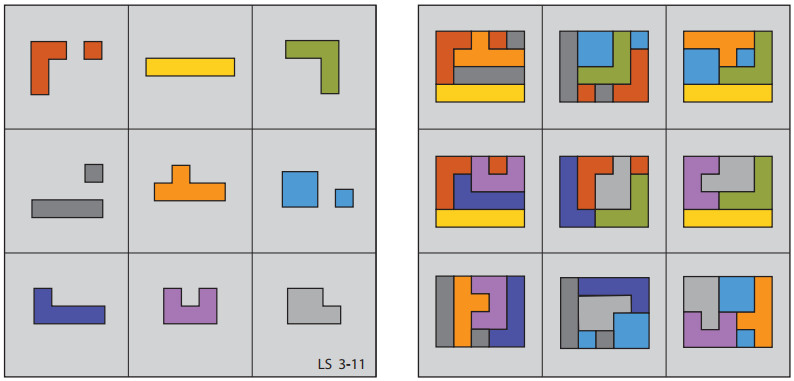
From Lee Sallows:
The traditional magic square is a square array of n×n distinct numbers, their magical property being that the sum of the n numbers occupying each row, column, and diagonal is the same. A variation on this theme that I introduced in 2011 is the geometric magic square in which distinct geometrical figures (usually planar shapes) occupy the cells of the array rather than numbers. The magical property enjoyed by such an array is then that the n shapes making up each row, column, and diagonal can be fitted together as in a jigsaw puzzle so as to yield (i.e. tile) a new compound shape that is the same in each case.
Beyond ‘ordinary’ geometric magic squares, it turns out that the combinative properties of shapes are such as to enable ‘magical’ constructions that are denied to analogous structures using numbers. For example, at left in the figure above is seen a 3×3 square of a kind that cannot be realized using distinct numbers rather than shapes. Note first that the square is to be understood as ‘toroidally-connected’, which is to say, as if inscribed on a torus. Its left-hand edge is then to be interpreted as adjacent to its right-hand edge and its top edge adjacent to its bottom edge. Its magical property is then that the four pieces contained within any 2×2 subsquare can be assembled to produce an identical shape, in this case a rectangle of size 4×5. In all there are nine such subsquares to be found in the square, as seen (again in a square) at right. Note that three of the pieces are disjoint, my attempts to produce a similar solution using nine unbroken pieces having failed. So whereas a 3×3 magic square, numerical or geometric, satisfies at least 8 separate conditions ( 3 rows + 3 columns + 2 diagonals), the square here shown satisfies one more.
(Thanks, Lee!)
