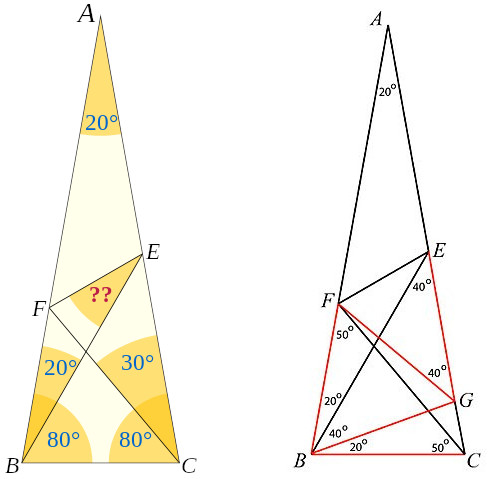
Edward Mann Langley, founder of the Mathematical Gazette, posed this problem in its pages in 1922:

ABC is an isosceles triangle. B = C = 80 degrees. CF at 30 degrees to AC cuts AB in F. BE at 20 degrees to AB cuts AC in E. Prove angle BEF = 30 degrees.

(Langley’s description makes no mention of D; perhaps this is at the intersection of BE and CF.)

A number of solutions appeared. One, offered by J.W. Mercer in 1923, proposes drawing BG at 20 degrees to BC, cutting CA in G. Now angle GBF is 60 degrees, and angles BGC and BCG are both 80 degrees, so BC = BG. Also, angles BCF and BFC are both 50 degrees, so BF = BG and triangle BFG is equilateral. But angles GBE and BEG are both 40 degrees, so BG = GE = GF. And angle FGE is 40 degrees, so GEF is 70 degrees and BEF is 30 degrees.